Bonjour
Je suis en galère sur un exercice d'entraînement de mathématiques
Nous avons surtout vu jusque là les ensembles, la récurrence et le télescopage.
Si vous pouviez m'aider, ce serait super !
Exercice 1.7 : les questions sont indépendantes.
1. Montrer que pour tout nEN*, 1/2< {Somme de k=1 à n} 1/n+k <1
2. Montrer que pour tout nEN*, 1/2 < {Somme de k=1 à n} n/(n^2)+k < 1
Merci d'avance !
Prepa MPSI Inéquation avec symbole somme
11 messages
- Page 1 sur 1
Re: Prepa MPSI Inéquation avec symbole somme
Bonjour Lucie,
essaie d'écrire avec les balises TEX accessibles dans l'éditeur :
Soit un entier supérieur ou égal à 1. Montrer :
un entier supérieur ou égal à 1. Montrer :
1.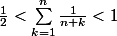
2.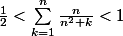
essaie d'écrire avec les balises TEX accessibles dans l'éditeur :
Soit
1.
2.
Re: Prepa MPSI Inéquation avec symbole somme
Tu as affaire ici à des sommes finies de nombres positifs.
Pour majorer la somme, essaie de majorer chaque terme.
Pour minorer la somme, essaie de minorer chaque terme.
D'ailleurs, peut-être as tu mal recopié l'énoncé et les inégalités sont au sens large?
Car si tu prends n=1 dans 1. ou dans 2. , chaque somme vaut 1/2, ce qui met en défaut l'inégalité stricte.
Pour majorer la somme, essaie de majorer chaque terme.
Pour minorer la somme, essaie de minorer chaque terme.
D'ailleurs, peut-être as tu mal recopié l'énoncé et les inégalités sont au sens large?
Car si tu prends n=1 dans 1. ou dans 2. , chaque somme vaut 1/2, ce qui met en défaut l'inégalité stricte.
Re: Prepa MPSI Inéquation avec symbole somme
En effet ce n'est pas au sens strict mais je n'avais pas d'autre symbole sur mon téléphone
Re: Prepa MPSI Inéquation avec symbole somme
LB2 a écrit:Tu as affaire ici à des sommes finies de nombres positifs.
Pour majorer la somme, essaie de majorer chaque terme.
Pour minorer la somme, essaie de minorer chaque terme.
D'ailleurs, peut-être as tu mal recopié l'énoncé et les inégalités sont au sens large?
Car si tu prends n=1 dans 1. ou dans 2. , chaque somme vaut 1/2, ce qui met en défaut l'inégalité stricte.
Oui donc chaque terme est compris entre 0 et 1 mais je ne vois pas où je peux aller avec..
Re: Prepa MPSI Inéquation avec symbole somme
L'encadrement entre 0 et 1 est trop grossier pour en tirer quelque chose.
A k fixé entre 1 et n, essaie d'encadrer le terme de rang k par des quantités qui ne dépendent que de n.
On parle d'encadrement uniforme en k.
Et ensuite, tu sommes ces encadrements (facile puisque tu sais sommer des constantes)
A k fixé entre 1 et n, essaie d'encadrer le terme de rang k par des quantités qui ne dépendent que de n.
On parle d'encadrement uniforme en k.
Et ensuite, tu sommes ces encadrements (facile puisque tu sais sommer des constantes)
Re: Prepa MPSI Inéquation avec symbole somme
LB2 a écrit:L'encadrement entre 0 et 1 est trop grossier pour en tirer quelque chose.
A k fixé entre 1 et n, essaie d'encadrer le terme de rang k par des quantités qui ne dépendent que de n.
On parle d'encadrement uniforme en k.
Et ensuite, tu sommes ces encadrements (facile puisque tu sais sommer des constantes)
D'accord merci donc la j'ai :
1 < k < n
1 + n < n+k < 2n
Ce que j'ai sommé et je tombe donc sur :
[n(n+1)/2] + n < Somme n+k < n(n+1)
Je dois donc ensuite faire l'inverse ? Car Si c'est le cas j'ai donc :
[2/n(n+1)] + 1/n > Somme 1/n+k > 1/n(n+1)
Suis je sur la bonne voie ?
Re: Prepa MPSI Inéquation avec symbole somme
Je crois que j 'ai compris ce qu'à écrit LB2
C'est simple en réalité: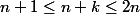 tu inverses cette inégalité puis en sommant tu te rendras compte que les deux sommes sont des constantes donc elles ne dépendent plus de k. Il suffit alors de multiplier par le nombre de terme
tu inverses cette inégalité puis en sommant tu te rendras compte que les deux sommes sont des constantes donc elles ne dépendent plus de k. Il suffit alors de multiplier par le nombre de terme
C'est simple en réalité:
Re: Prepa MPSI Inéquation avec symbole somme
fastandmaths a écrit:Je crois que j 'ai compris ce qu'à écrit LB2
C'est simple en réalité:tu inverses cette inégalité puis en sommant tu te rendras compte que les deux sommes sont des constantes donc elles ne dépendent plus de k. Il suffit alors de multiplier par le nombre de terme
Merci Beaucoup
Re: Prepa MPSI Inéquation avec symbole somme
fastandmaths a écrit:Je crois que j 'ai compris ce qu'à écrit LB2
C'est simple en réalité:tu inverses cette inégalité puis en sommant tu te rendras compte que les deux sommes sont des constantes donc elles ne dépendent plus de k. Il suffit alors de multiplier par le nombre de terme
Tout à fait, et cela fonctionne de la même façon pour la somme 2
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
