Bonjour à tous,
J'ai un projet d'informatique à faire et je bloque à un niveau : j'ai la position de deux points et la longueur des deux autres côtés (je connais implicitement les trois longueurs) et je cherche à trouver la position du troisième point du triangle.
Merci par avance et bonne soirée.
Position du 3éme point d'un triangle
4 messages
- Page 1 sur 1
Salut,
Si tu connait A et B et que tu cherche C tel que AC=b (connu) et BC=a (connu), il te suffit d'écrire le système formé par ces deux équation (que tu élève au carré pour virer les racines carrées) pour trouver les deux solutions (symétrique l'une de l'autre par rapport à la droite (AB) ).
Et évidement, vu qu'il y a deux solution, ça signifie que tu va avoir... une équation du second degré à résoudre.
Si tu connait A et B et que tu cherche C tel que AC=b (connu) et BC=a (connu), il te suffit d'écrire le système formé par ces deux équation (que tu élève au carré pour virer les racines carrées) pour trouver les deux solutions (symétrique l'une de l'autre par rapport à la droite (AB) ).
Et évidement, vu qu'il y a deux solution, ça signifie que tu va avoir... une équation du second degré à résoudre.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
J'avais tenté le système mais le problème c'est que l'équation est plutôt compliquée à résoudre (pour moi du moins :)). J'ai tenté une résolution sur maple mais je me retrouve avec des équations de positions plutôt longues (plus ou moins 1/2 page par coordonnée). N'y a t-il pas une relation plus simple ? J'ai aussi tenté d'utiliser le théorème d'al cachy mais je me retrouve à devoir calculer un angle de passage que j'aurais préféré éviter de voir apparaître dans mon programme. Merci quand même d'avoir pris le temps de me répondre !
En fait, il y a plus simple pour les calculs.
 sont connus ainsi que les points
sont connus ainsi que les points 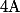 et
et 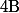 .
.
Les vecteurs\) et
et \) sont connus, orthogonaux et de même norme
sont connus, orthogonaux et de même norme 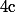 .
.
Si on cherche le point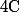 sous la forme
sous la forme 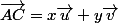 alors on a :
alors on a :
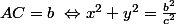 et
et 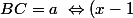^2+y^2=\frac{a^2}{c^2}\)
La première équation moins la deuxième donne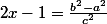 donc
donc 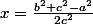
Et la première donne ensuite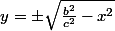 (avec
(avec 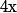 que tu as déjà calculé)
que tu as déjà calculé)
Bilan :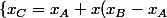 -y(y_B-y_A)\cr y_C=y_A+x(y_B-y_A)+y(x_B-x_A)}\right.)
Les vecteurs
Si on cherche le point
La première équation moins la deuxième donne
Et la première donne ensuite
Bilan :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
