Bonjour je cherche à connaitre les polynômes irréductible unitaire dans F_3[X] et pour moi il suffit de trouver a et b dans F_3 tel que pour P(X) = X²+aX+b alors P(0),P(1), et P(2) e soient différents de 0. Ainsi j'obtient les polynômes suivant :
X²+1
X²+X+2
X²+2X+2
Mais d'après mes recherches j'ai l'impression que ce n'est pas totalement juste... Pourriez vous me guider, ou me dire où mon raisonnement est faux ! Je vous remercie d'avance!!
Polynome irréductibles unitaire dans F_3[X]
8 messages
- Page 1 sur 1
Re: Polynome irréductibles unitaire dans F_3[X]
Bonjour,
Il y a des polynômes unitaires irréductibles en chaque degré. Alors que cherches-tu exactement ? Ceux de degré 2 ?
On sait de manière générale qu'un polynôme de degré 2 ou 3 sur un corps
est irréductible sur si et seulement s'il n'a pas de racine (c.-à-d. pas de facteur du premier degré) dans
si et seulement s'il n'a pas de racine (c.-à-d. pas de facteur du premier degré) dans  .
.
Il y a des polynômes unitaires irréductibles en chaque degré. Alors que cherches-tu exactement ? Ceux de degré 2 ?
On sait de manière générale qu'un polynôme de degré 2 ou 3 sur un corps
est irréductible sur
Re: Polynome irréductibles unitaire dans F_3[X]
(X^2+1)^2 est réductible mais sans racine .
Il en va de même de toutes les puissances d'exposant supérieur à 1 de tous les polynômes irréductibles.
Si il y a une cns d'irreductibilité pour les polynômes unitaires de F3[X] , on est dans l'algèbre++
Il en va de même de toutes les puissances d'exposant supérieur à 1 de tous les polynômes irréductibles.
Si il y a une cns d'irreductibilité pour les polynômes unitaires de F3[X] , on est dans l'algèbre++
Re: Polynome irréductibles unitaire dans F_3[X]
C'est bien pour ça que j'ai écrit : de degré 2 ou 3.
Re: Polynome irréductibles unitaire dans F_3[X]
Ma troisième ligne n'était , et est toujours une question implicite à ton adresse.
Re: Polynome irréductibles unitaire dans F_3[X]
Il y a des algorithmes pour décider si un polynôme sur un corps fini est irréductible (il y a des algorithmes pour factoriser en facteurs irréductibles).
On peut factoriser en facteurs irréductibles unitaires. Les facteurs de degré
en facteurs irréductibles unitaires. Les facteurs de degré  donnent la liste des polynômes irréductibles unitaires de degré
donnent la liste des polynômes irréductibles unitaires de degré  .
.
Pour , ceci dit qu'on a trois polynômes irréductibles unitaires de degré 2.
, ceci dit qu'on a trois polynômes irréductibles unitaires de degré 2.
On peut factoriser
Pour
Re: Polynome irréductibles unitaire dans F_3[X]
Merci à toi.
On dispose donc d'un algorithme pour déterminer la liste des polynômes irréductibles unitaires de degré donné .
J'ai vérifié que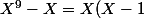(X+1)(X^2+1)(X^2+2X+2)(X^2+X+2))
On dispose donc d'un algorithme pour déterminer la liste des polynômes irréductibles unitaires de degré donné .
J'ai vérifié que
Re: Polynome irréductibles unitaire dans F_3[X]
De plusieurs algorithmes, même.
Il y en a un tout à fait bête, par récurrence :
En chaque degré il y a un nombre fini de polynômes unitaires. On fait la liste des polynômes unitaires de degré qui sont des produits de polynômes unitaires de degrés strictement inférieurs. Les autres sont irréductibles.
qui sont des produits de polynômes unitaires de degrés strictement inférieurs. Les autres sont irréductibles.
Il y en a un tout à fait bête, par récurrence :
En chaque degré il y a un nombre fini de polynômes unitaires. On fait la liste des polynômes unitaires de degré
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
