Plan, sous-espace vectoriel.
13 messages
- Page 1 sur 1
Plan, sous-espace vectoriel.
Bonjour
Comment montrer en détail qu'un plan P est un sous-espace vectoriel.
Dois-t-on réaliser un calcul ?
A bientôt
Comment montrer en détail qu'un plan P est un sous-espace vectoriel.
Dois-t-on réaliser un calcul ?
A bientôt
Re: Plan, sous-espace vectoriel.
Bonsoir
Voici les trois points.
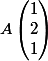 ,
, 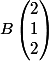 ,
, 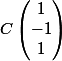
Avec ces points j'ai trouver l'équation cartésienne du plan (P)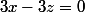 .
.
Les calculs détaillés se trouvent dans ce poste.
superieur/equation-cartesienne-plan-avec-trois-points-t235741.html
J'ai eu une folle idée pour montrer que le plan P est un sous-espace vectoriel.
On devrait démontrer que les trois points forment un sous espace-vectoriel.
Voici les calculs.
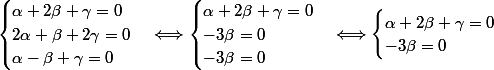
Est-ce que mon calcul est correct ?
Est-ce que les trois points forment un sous-espace vectoriel ?
A bientôt
Voici les trois points.
Avec ces points j'ai trouver l'équation cartésienne du plan (P)
Les calculs détaillés se trouvent dans ce poste.
superieur/equation-cartesienne-plan-avec-trois-points-t235741.html
J'ai eu une folle idée pour montrer que le plan P est un sous-espace vectoriel.
On devrait démontrer que les trois points forment un sous espace-vectoriel.
Voici les calculs.
Est-ce que mon calcul est correct ?
Est-ce que les trois points forment un sous-espace vectoriel ?
A bientôt
Re: Plan, sous-espace vectoriel.
Bonjour
J'ai réfléchi cette nuit, j'en ai déduit que mes calculs ci-dessus pour montrer que le plan P est un sous-espace vectoriel sont faux.
Là, je suis perdue.
Quelle méthode doit-je employer ?
A bientôt
J'ai réfléchi cette nuit, j'en ai déduit que mes calculs ci-dessus pour montrer que le plan P est un sous-espace vectoriel sont faux.
Là, je suis perdue.
Quelle méthode doit-je employer ?
A bientôt
Re: Plan, sous-espace vectoriel.
Bonjour,
Tu as l'équation de ton plan :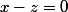 (le facteur 3 ne sert à rien). Est-ce si difficile de démontrer que l'ensemble des
(le facteur 3 ne sert à rien). Est-ce si difficile de démontrer que l'ensemble des ) de
de 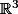 qui vérifient
qui vérifient 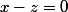 est un sous-espace vectoriel ?
est un sous-espace vectoriel ?
Tu as l'équation de ton plan :
Re: Plan, sous-espace vectoriel.
Ah ! Je mérite des claques.
On suppose que P est une sous-espace vectoriel.
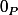
=x-z =0-0=0)
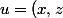) et
et 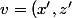) appartiennent à P alors
appartiennent à P alors 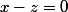 et
et 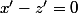 on en déduit que
on en déduit que +(x'-z')=0) ainsi
ainsi 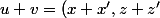\in P)
On a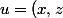) et
et 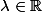 donc
donc 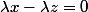 alors
alors 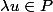
Le plan P est bien un sous-espace vectoriel.
Est-ce que les calculs sont correct ?
A bientôt
On suppose que P est une sous-espace vectoriel.
On a
Le plan P est bien un sous-espace vectoriel.
Est-ce que les calculs sont correct ?
A bientôt
Re: Plan, sous-espace vectoriel.
Oui mais les éléments de P sont des triplets (x,y,z) donc revoir la rédaction, même si pour les calculs y n'intervient pas...
Re: Plan, sous-espace vectoriel.
Bonsoir
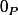
=3x+y-3z = 3.0+0-3.0=0)
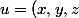) et
et 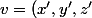) appartiennent à P alors
appartiennent à P alors 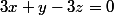 et
et 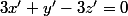 donc
donc  + (3x'+y'-3z')=0) ainsi
ainsi  \in P)
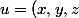) et
et 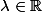 don
don 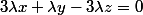 alors
alors 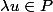
Est-ce que c'est correct ?
A bientôt
Est-ce que c'est correct ?
A bientôt
Re: Plan, sous-espace vectoriel.
Mais non vous avez changé l'équation du plan !!
C'est x-z=0
Au début O(0,0,0) appartient à P car ses cordonnées vérifient l'équation
C'est x-z=0
Au début O(0,0,0) appartient à P car ses cordonnées vérifient l'équation
Re: Plan, sous-espace vectoriel.
Bonjour
Je suis un peu perdu là !
\in P)
=0-0= 0)
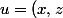) et
et 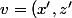) appartiennent à P alors
appartiennent à P alors 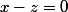 et
et 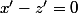 donc
donc +(z+z')=0) ainsi
ainsi 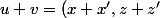 \in P)
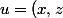) et
et 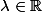 donc
donc 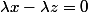 ce qui donne
ce qui donne 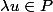
Est-ce que là c'est correct ?
A bientôt
Je suis un peu perdu là !
Est-ce que là c'est correct ?
A bientôt
Re: Plan, sous-espace vectoriel.
Les éléments de P ont trois coordonnées
Donc soit u(x,y,z) et v(x',y',z'), ils sont dans P donc x-z=0 et x'-z'=0...etc
Même si y n'intervient pas dans l'équation il faut quand même l'écrire quand on définit les vecteurs.
Donc soit u(x,y,z) et v(x',y',z'), ils sont dans P donc x-z=0 et x'-z'=0...etc
Même si y n'intervient pas dans l'équation il faut quand même l'écrire quand on définit les vecteurs.
Re: Plan, sous-espace vectoriel.
D'autre part ce n'est pas (x+x')+(y+y')=0
mais (x+x')-(y+y')=0 ce qui permet de dire que u+v est dans P
mais (x+x')-(y+y')=0 ce qui permet de dire que u+v est dans P
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
