Plan affine / Plan vectoriel

par **barbu23** » 27 Déc 2009, 16:58

Bonjour à tous : :happy3:
Quelle est la difference entre un plan vectoriel ( appartenant à un espace vectoriel

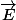
) et un plan affine ( appartenant à un espace affine

)
Par exemple dans

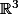
( l'espace affine à

dimension ) : le plan

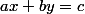
est un plan affine de l'espace affine

.
Si on note :

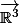
l'espace vectoriel associé à l'espace affine

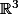
. Quel est l'equivalent du plan

dans l'espace vectoriel

?
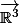
Merci d'avance ! :happy3:

par **Nightmare** » 27 Déc 2009, 17:01

Un plan affine c'est juste un plan vectoriel qui a subit une translation. Le plan vectoriel contient 0 (comme tout espace vectoriel qui se respecte).

par **barbu23** » 27 Déc 2009, 17:25

Oui, et comment on ecrit l'equation d'un plan vectoriel associé au plan affine

?
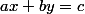
Merci d'avance ! :happy3:

par **XENSECP** » 27 Déc 2009, 17:40

Bah simplement

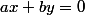
dans l'espace bien sûr. Car il faut que le vecteur nul soit dans le plan, ie (0;0;0) vérifie ton équation.

par **barbu23** » 27 Déc 2009, 17:47

c'est quoi

?

par **XENSECP** » 27 Déc 2009, 17:49

barbu23 a écrit:c'est quoi ?

Euh le vecteur nul quoi :

par **barbu23** » 27 Déc 2009, 18:04

Je comprends pas malheureusement ! tu peux detailler un peu plus c'ke que tu veux dire : XENSECP, pour que j'comprends bien ? :hum:
Merci d'avance ! :happy3:

par **Nightmare** » 27 Déc 2009, 18:05

Tu ne sais pas ce qu'est (0,0,0) ? Je ne comprends pas dans quel ordre tu as introduit tes notions mathématiques depuis quelques années mais surement pas dans le bon. Je t'invite à reprendre les bases avant de continuer, car à la vue de tes postes ton niveau est vraiment bas par rapport à la hauteur des questions...

par **barbu23** » 27 Déc 2009, 18:13

Oui, mais que faire, j'ai pas le choix maintenant, j'ai besoin d'une reponse clair ! :cry:
Merci d'avance ! :happy3:
P.D : J'ai presque tout oublié sur les espaces projectives, car on ne l'utilisait depuis plusieurs années ! :happy3:

par **XENSECP** » 27 Déc 2009, 18:21

Je t'ai dit ce que c'était la réponse ;)

par **barbu23** » 27 Déc 2009, 18:23

Oui, mais assez clairement stp ! j't'en supplie ! :cry: :happy3:

par **sniperamine** » 27 Déc 2009, 21:07

barbu23 a écrit:Oui, mais assez clairement stp ! j't'en supplie ! :happy3:

dans R3 un espace de dimension 3 tu as les coordonnées (x,y,z) trois axes donc le vecteur nul 0 = (0,o,o) pour x=y=z=0 dans un plan tu as (x,y) 2 axes dans un repère l'axe des coordonnées et des abscisses etc etc

par **barbu23** » 27 Déc 2009, 21:22

Merci sniperman ! :happy3:

par **Nightmare** » 27 Déc 2009, 21:35

barbu23 a écrit:Oui, mais que faire, j'ai pas le choix maintenant, j'ai besoin d'une reponse clair !
Merci d'avance ! :happy3:

Franchement, c'est aberrant...

par **alavacommejetepousse** » 27 Déc 2009, 21:38

bonsoir
une remarque

il semblerait que dans ce post seuls les ev soient munis d une structure d ea sans doute serait il plus clair pour barbu de distinguer point et vecteur

Plan affine / Plan vectoriel

Plan affine / Plan vectoriel

Qui est en ligne