Bonjour à tous,
Je me trouve devant un problème d'optimisation d'une fonction dont l'ensemble de définition est discret (N ou Z en l'occurence), et je ne sais par quel bout le prendre.
On me donne 5 nombres 1, 3 ,5, 9, et 20 et l'expression A=(a+c)(b+d)e. Et on me demande d'optimiser A sachant que a,b,c,d,e sont affectés de manière univoque aux 5 nombres ci-dessus. Il y a 5! combinaisons de 5-uplets à essayer. Mais je suis sûr que cette methode laborieuse n'est pas la bonne. Il y a une astuce sans doute qui réduirait le nombre d'essais. Quelqu'un a-t-il une idée d'une methode générale pour résoudre ce genre de problème ?
Optimisation discrète
9 messages
- Page 1 sur 1
Re: Optimisation discrète
Bonjour,
Pour une étude exhaustive il suffit en fait de calculer dans 5 x 6 = 30 situations. Ça fait déjà quatre fois moins.
Pour une étude exhaustive il suffit en fait de calculer dans 5 x 6 = 30 situations. Ça fait déjà quatre fois moins.
Re: Optimisation discrète
Oui, à cause des symetries entre a et b induites par a+b et ditto pour c et d. Mais faut-il se farcir 30 combinaisons pour avoir les valeurs maxi et mini de A? J'ai trouvé comme maxi 1600, mais en tatonnant (et je ne suis pas sûr que c'est vraiment un maxi et s'il est unique) Quant au mini, je ne me suis pas encore attelé à la tache. Ma méthode n'est pas très mathématique! N'y a-t-il pas moyen de rendre le problème "continu" et de travailler sur A comme sur une "bonne" fonction en cherchant à annuler les dérivées partielles ?
Re: Optimisation discrète
Tu peux trouver les valeurs de 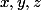 réels
réels 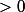 qui maximisent le produit
qui maximisent le produit 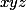 pour
pour 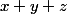 constant.
constant.
Tu peux t'en approcher le plus possible avec les cinq entiers qui te sont donnés.
Tu peux t'en approcher le plus possible avec les cinq entiers qui te sont donnés.
Re: Optimisation discrète
J'ai suivi le raisonnement suivant:
la somme de a+b+c+d+e= 38 et je pose x=a+c et y = b+d
Il s'en suit que e=38-x-y
A peut donc s'écrire : A=x*y*(38-x-y) et la dérivée de A par rapport à x donne :
dA/dx= 38y-2xy-y²
dA/dy=38x-x²-2xy
Un optimum est obtenu si dA/dx=dA/dy=0, ce qui nous amène à résoudre le système 2x+y=38 et 2y+x=38 et entraine x=y=38/3=12.66
J'ai raisonné en randant la fonction continue sur un ensemble continu! Il ne reste donc plus qu'à composer les couples x=(a,c) et y=(b,d) de manière que a+c et b+d soient le plus proches de 12.66. Les couples (5,3) et (1,9) sont ceux dont les sommes de leurs composantes se rapprochent le plus de 12.66. D'où : A=(3+5)(1+9)20=1600 serait un maximum.
Mon raisonnement est-il juste ?
NB Les couples (9,3) et (5,1) dont les sommes respectives des composantes sont 12 et 6 connaissent un écart trop grand par rapport à la condition x=y=12.66 et donnent A=12*6*20=1440 <1600 !
la somme de a+b+c+d+e= 38 et je pose x=a+c et y = b+d
Il s'en suit que e=38-x-y
A peut donc s'écrire : A=x*y*(38-x-y) et la dérivée de A par rapport à x donne :
dA/dx= 38y-2xy-y²
dA/dy=38x-x²-2xy
Un optimum est obtenu si dA/dx=dA/dy=0, ce qui nous amène à résoudre le système 2x+y=38 et 2y+x=38 et entraine x=y=38/3=12.66
J'ai raisonné en randant la fonction continue sur un ensemble continu! Il ne reste donc plus qu'à composer les couples x=(a,c) et y=(b,d) de manière que a+c et b+d soient le plus proches de 12.66. Les couples (5,3) et (1,9) sont ceux dont les sommes de leurs composantes se rapprochent le plus de 12.66. D'où : A=(3+5)(1+9)20=1600 serait un maximum.
Mon raisonnement est-il juste ?
NB Les couples (9,3) et (5,1) dont les sommes respectives des composantes sont 12 et 6 connaissent un écart trop grand par rapport à la condition x=y=12.66 et donnent A=12*6*20=1440 <1600 !
Re: Optimisation discrète
Si on veut quelque chose de vraiment probant, on peut procéder ainsi :
On choisit un des 5 pour aller tout seul (faire le e). On sait que le produit des deux autres facteurs a+b et c+d sera le plus grand possible si on est le plus proche possible de moitié-moitié.
Ça donne
1- pour e=20 : 10 et 8
2- pour e=9 : 21 et 8
3- pour e=5 : 21 et 12
4 : pour e=3 : 21 et 14
5 : pour e=1 : 23 et 14
Ensuite : les 4 et 5 ont en commun un facteur 14, et (21,3) est plus proche du moitié-moitié que (23,1). Donc le 4 est plus grand que le 5.
Pour la même raison on voit que parmi les 2,3,4 qui ont un facteur 21 en commun, c'est le 2 le plus grand.
Le 1 et le 2 ont un facteur 8 en commun, et c'est le 1 le plus grand, qui est donc le plus grand de tous.
On peut suivre la même démarche pour trouver le plus petit
On choisit un des 5 pour aller tout seul (faire le e). On sait que le produit des deux autres facteurs a+b et c+d sera le plus grand possible si on est le plus proche possible de moitié-moitié.
Ça donne
1- pour e=20 : 10 et 8
2- pour e=9 : 21 et 8
3- pour e=5 : 21 et 12
4 : pour e=3 : 21 et 14
5 : pour e=1 : 23 et 14
Ensuite : les 4 et 5 ont en commun un facteur 14, et (21,3) est plus proche du moitié-moitié que (23,1). Donc le 4 est plus grand que le 5.
Pour la même raison on voit que parmi les 2,3,4 qui ont un facteur 21 en commun, c'est le 2 le plus grand.
Le 1 et le 2 ont un facteur 8 en commun, et c'est le 1 le plus grand, qui est donc le plus grand de tous.
On peut suivre la même démarche pour trouver le plus petit
Re: Optimisation discrète
OK, je comprends ton raisonnement. Mais si l'expression A changeait et était plus compliquée du genre A=a²-bc²+d/e, comment fait-on ? On se tape les 120 (=5!) combinaisons de a,b,c,d,e ? Il ne faut pas oublier que l'on a bénéficier de la symétrie des facteurs a+c et b+d pour réduire la complexité ! N'y a-t-il pas une méthode générale pour ce genre de problème ?
Re: Optimisation discrète
"On se tape les 120 (=5!) combinaisons de a,b,c,d,e ?"
Ce n'est pas si compliqué que ça, avec un petit programme ça ira vite.
Ce n'est pas si compliqué que ça, avec un petit programme ça ira vite.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 99 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
