Non majoration d'une suite récurrente

[Hyp]

Bonsoir à tous :)

Ayant une suite récurrence tel que : U0=0 et U(n+1)=f(Un), avec f:x--> X²+A.

Ayant Un croissante pour tout A positif, comment peut on montrer que Un tend vers l'infini pour tout A>1/4 ?

Il suffit évidemment de montrer que Un est non majorée :

On la suppose alors majorée pour aboutir à une contradiction, ce qui donne:

Il existe M dans IR tel que pour tout n dans IN, Un <= M

On pose M' = M-;), qui n'est plus un majorant de Un

Mais je bloque pour choisir N tel que UN > M' =x

Merci de votre aide :happy2:

[Nightmare]

Salut :happy3:


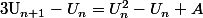
Le discriminant vaut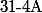 (Comme par hasard :lol3:)

Ainsi si A > 1/4 le discriminant est négatif et la différence est alors positive. La suite est donc croissante.

Supposons qu'elle converge, alors elle converge vers un point fixe de f, ie un l tel que l²+A=l

Essaye de montrer que f est plus grand que le plus grand point fixe à partir d'un certain rang.

[Hyp]

Mais si on aboutit à une contradiction, on aurait que Un diverge, or il est demandé de montrer qu'elle tend vers l'infini (plus précisément).

Et on sait qu'elle est déjà croissante :)

[Nightmare]

Une suite croissante peut soit converger, soit tendre vers l'infini :happy3:

[ffpower]

ben une suite croissante,soit ca tend vers l infini,soit ca converge....et si ca convergeait ce serait vers un point fixe de f,or f n a pas de points fixes..

[Nightmare]

Euh oui... pourquoi étudier les points fixe quand il n'y en a pas ...

[Hyp]

Mais ça me parait incomplet de dire qu'elle diverge car f n'admet aucun point fixe :hein:

[Nightmare]

Bah non c'est logique.
Si la suite convergeait, ce serait vers un point fixe de f par continuité. Or f n'admet pas de point fixe, la suite diverge donc. Comme elle est croissante, elle diverge vers +oo.

[Hyp]

Mais c'est tellement puissant que ça mérite le titre de théorème :doh:

Bref, ce n'est peut être pas la méthode voulue, mais merci bien :we:

[Nightmare]

C'est la méthode la plus simple...

[Hyp]

Oui c'est bien évident, mais vu l'esprit de l'exo je m'attendais pas à ça.
Ils cherchent toujours à compliquer les choses, "eux" :p.

Ah, juste une dernière question s'il vous plait :

pour A dans [0,1/4[, on m'indique qu'il faut choisir un intervalle stable par f pour montrer la convergence de Un (et j'ai le résultat que si I est stable par f, alors dès que U0 dans I, Un dans I ). Mais je vois pas du tout :cry:

[Nightmare]

A priori un intervalle qui semblerait stable par f, ça laisse penser aux points fixe.
Regarde l'intervalle formé des deux points fixe. Est-il stable?

[Hyp]

Très, merci :we:

Ca ira si je les pose X et X' par exemple, juste par commodité ?

[Nightmare]

Bien sûr, ce ne sont pas les notations qui doivent poser problème dans un exercice :lol3:

[ffpower]

Bon,premierement f est croissante sur R+.Comme u(1)=A superieur a u(0)=0,en appliquant f on a u(2) superieur a u(1) puis par reccurence u(n+1) superieur a u(n).la suite est donc encore croissante dans ce cas la.

Ensuite,f a 2 points fixes(eventuellement confondus),qui sont positifs(ils se calculent aisément).Notons les r et r',avec r inferieur a r'.
On a u(0) inferieur a r,donc en appliquant f,on obtient u(1) inferieur a f(r)=r puis par recurrence u(n) inferieur a r.la suite u(n)est croissante et majorée par r,donc converge,disons vers l.l est un point fixe de f verifiant l inferieur a r,donc l=r

[Hyp]

Bonsoir, c'est encore moi :we:

Je pense avoir commis une faute de raisonnement, mais je ne vois pas comment. (Ou sinon l'énoncé est faux).

On a deux suites U2n, U2n+1, décroissante, respectivement croissantes, avec toujours : U0= 0. Un+1=f(Un), et f(x)=x²+A. Elles convergent vers a, respectivement vers b, tq fof (a)=a, et fof(b)=b (logique).

On demande de montrer que si A dans ]-3/4,0[, alors les deux suites convergent vers une même limite, puis la déduction évidente de la limite de Un.

On a déjà montré que fof(x)-x = (x²-x+A)(x²+x+A+1).


Voici le problème:

Je me suis basé sur le fait que si U2n décroit et converge, alors sa limite est nécessairement inférieure ou égale à son 1er terme, soit 0. De même, si U2n+1 croit, alors sa limite sera supérieure ou égale à U1, soit A.

Il s'agirait par la suite de résoudre la polynôme (x²-x+A)(x²+x+A+1).
(x²+x+A+1) est toujours positif et ne s'annule pas pour les valeurs précisées de A.

Par contre (x²-x+A) s'annule en deux points, (éventuellement confondus ?).

Donc la limite de U2n est nécessairement négative, on élimine alors une racine positive (1+(racine(1-4A)/2).

Logiquement, on doit éliminer la même racine pour U2n+1 si on procède de la même manière, sauf que dans ce cas là, c'est la racine déjà éliminée qui persiste..

Merci de votre aide :)

[alavacommejetepousse]

bonsoir

l'intervalle

[A,0] est stable par f comme u0 = 0 la suite u est valeurs négatives

donc les limites de u2n et u2n+1 également les racines de x^2-x +A étant de signe contraire une seule est à garder.

[Hyp]

Et si A dans ]-1;-3/4[, les racines prennent 3 valeurs négatives, mais comment justifier que les deux suites ne peuvent pas prendre la même valeur ?

[alavacommejetepousse]

je t'en prie

[Hyp]

Le prends pas mal, j'allais quand même pas rien dire mais comme j'avais encore une question :wrong: ..

Merci quand même ^^