Montrer qu'un polynôme B divise un polynôme A
60 messages
- Page 1 sur 3 - 1, 2, 3
Montrer qu'un polynôme B divise un polynôme A
Bonsoir à tous,
Je rencontre un problème sur l'exercice suivant:
On note pour tout n appartenant à N*: Pn = X^2^n + X^2^(n-1) + 1 appartenant à R[X]
Montrer pour tout (n, m) appartenant à N*^2, n inférieure ou égale à m ==> Pn divise Pm.
J'ai traité le cas n = m. Dans ce cas Pn est égal à Pm. Donc Pn divise Pm.
C'est le cas n < m qui me pose problème. Je dois montrer que Pm = PnQ mais je n'arrive pas à faire cela. Je pense qu'il y a une astuce que je ne vois pas. Quelqu'un pourrait m'aider ?
Merci d'avance !
Je rencontre un problème sur l'exercice suivant:
On note pour tout n appartenant à N*: Pn = X^2^n + X^2^(n-1) + 1 appartenant à R[X]
Montrer pour tout (n, m) appartenant à N*^2, n inférieure ou égale à m ==> Pn divise Pm.
J'ai traité le cas n = m. Dans ce cas Pn est égal à Pm. Donc Pn divise Pm.
C'est le cas n < m qui me pose problème. Je dois montrer que Pm = PnQ mais je n'arrive pas à faire cela. Je pense qu'il y a une astuce que je ne vois pas. Quelqu'un pourrait m'aider ?
Merci d'avance !
Re: Montrer qu'un polynôme B divise un polynôme A
Bonsoir,
Peux-tu démontrer que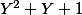 divise
divise 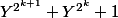 ?
?
Après, tu pourras chercher le bon et le bon
et le bon  .
.
Peux-tu démontrer que
Après, tu pourras chercher le bon
Re: Montrer qu'un polynôme B divise un polynôme A
Comment as-tu eu l'idée de faire cela ? Je vois que tu pars d'une valeur "simple" à calculer n = 1. Mais pourquoi X^2^(k+1) ?
Je pose la division:
X^2^(k+1) + X^2^k + 1 = (X^2 + X + 1)Q
Je crois que je suis gêné par les puissances de puissance. Je vois bien qu'il faut que le plus grand exposant de Q soit 2^(k+1).
Naïvement, j'ai fait:
X^2^(k+1) = X^(2k+2) selon la règle (A^b)^c = A^bc. Mais quand je pose mon équation ainsi, ça ne va pas...
Je pose la division:
X^2^(k+1) + X^2^k + 1 = (X^2 + X + 1)Q
Je crois que je suis gêné par les puissances de puissance. Je vois bien qu'il faut que le plus grand exposant de Q soit 2^(k+1).
Naïvement, j'ai fait:
X^2^(k+1) = X^(2k+2) selon la règle (A^b)^c = A^bc. Mais quand je pose mon équation ainsi, ça ne va pas...
Re: Montrer qu'un polynôme B divise un polynôme A
L'idée de voir ce qui se passe pour n=1 me semble assez naturelle. Non, pas pour toi ?
Pense aux racines ! C'est quoi, les racines de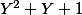 ?
?
Tu te mélanges grave les pinceaux entre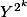 et
et ^k=Y^{2k}) , j'ai l'impression.
, j'ai l'impression.
Pense aux racines ! C'est quoi, les racines de
Tu te mélanges grave les pinceaux entre
Re: Montrer qu'un polynôme B divise un polynôme A
Oui, tout à fait d'accord mais je manque de visibilité, c'est pour ça que je posais cette question. Ca ne me dit pas pourquoi tu as choisi X^2^(k+1).
Les racines x, y sont x = (-1 + i )/2 et y = (-1 - i
)/2 et y = (-1 - i  )/2).
)/2).
Oui ce n'est pas qu'une impression. Je ne vois pas comment traiter X^2^k...
Les racines x, y sont x = (-1 + i
Oui ce n'est pas qu'une impression. Je ne vois pas comment traiter X^2^k...
Re: Montrer qu'un polynôme B divise un polynôme A
Ce que j'ai fait:
J'ai dégagé les deux racines comme indiqué ci-dessus.
Si est une racine de P alors X -
est une racine de P alors X -  divise P.
divise P.
Or les deux racines divisent à la fois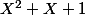 et X^2^(k+1) +
et X^2^(k+1) + 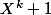 . Donc on peut réécrire les deux polynômes sous la forme deux polynômes scindés. On peut diviser par (X - (-1 + i
. Donc on peut réécrire les deux polynômes sous la forme deux polynômes scindés. On peut diviser par (X - (-1 + i )/2) ou par (X - (-1 -i
)/2) ou par (X - (-1 -i )/2). Donc
)/2). Donc 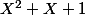 divise X^2^(k+1)
divise X^2^(k+1) 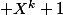 .
.
Qu'en penses-tu ?
J'ai dégagé les deux racines comme indiqué ci-dessus.
Si
Or les deux racines divisent à la fois
Qu'en penses-tu ?
Re: Montrer qu'un polynôme B divise un polynôme A
J'en pense que pour le moment je ne vois pas de démonstration du fait que  et
et  (connais-tu ces notations ?) sont des racines de
(connais-tu ces notations ?) sont des racines de 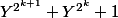 .
.
Erreur de vocabulaire : " les deux racines divisent ...".
Erreur de vocabulaire : " les deux racines divisent ...".
Re: Montrer qu'un polynôme B divise un polynôme A
Je ne comprends pas ce que tu veux dire par  et
et  sont des racines du polynôme y^2^(k+1) + y^2^k + 1.
sont des racines du polynôme y^2^(k+1) + y^2^k + 1.
Les deux racines que j'ai indiquées sont bien des racines de y^2^(k+1) + y^2^k + 1, non ?
Les deux racines que j'ai indiquées sont bien des racines de y^2^(k+1) + y^2^k + 1, non ?
Re: Montrer qu'un polynôme B divise un polynôme A
Je suis bien d'accord, mais tu ne donnes aucune démonstration de ce fait. Il ne suffit pas d'affirmer en mathématiques. Il faut démontrer.
Je t'ai demandé si tu connais la notation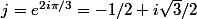 . Peux-tu répondre ?
. Peux-tu répondre ?
Je t'ai demandé si tu connais la notation
Re: Montrer qu'un polynôme B divise un polynôme A
Je suis tout à fait d'accord avec toi mais je prétends en avoir donner une démonstration. J'ai écrit que /2) et
et /2) sont racines de
sont racines de 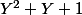 . Par conséquent
. Par conséquent 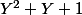 peut s'écrire comme
peut s'écrire comme /2)(X - (-1 - i\sqrt{3})/2)) . Donc
. Donc
y^2^(k+1) + y^2^k + 1 =/2)(X - (-1 - i\sqrt{3})/2)) Q
Q
Or si on prend la valeur/2) ou
ou /2) pour X, on aura:
pour X, on aura:
y^2^(k+1) + y^2^k + 1 = 0
Donc/2) et
et /2) sont des racines de y^2^(k+1) + y^2^k + 1. Ce qui signifie que ce polynôme peut se décomposer en produit de polynômes:
sont des racines de y^2^(k+1) + y^2^k + 1. Ce qui signifie que ce polynôme peut se décomposer en produit de polynômes: /2)(X - (-1 - i\sqrt{3})/2 )...) . Je ne sais pas combien il y a de racines, mais cela ne me semble pas très important pour la suite.
. Je ne sais pas combien il y a de racines, mais cela ne me semble pas très important pour la suite.
On peut donc diviser y^2^(k+1) + y^2^k + 1 par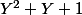
Ma démonstration est peut-être fausse mais il s'agit bien d'une démonstration.
Visiblement, il y a quelque chose qui te gêne là-dedans, je peine à le comprendre.
Hum, non cela ne me dit rien. Je t'avoue que je ne vois pas pourquoi tu penses à cela...
y^2^(k+1) + y^2^k + 1 =
Or si on prend la valeur
y^2^(k+1) + y^2^k + 1 = 0
Donc
On peut donc diviser y^2^(k+1) + y^2^k + 1 par
Ma démonstration est peut-être fausse mais il s'agit bien d'une démonstration.
Visiblement, il y a quelque chose qui te gêne là-dedans, je peine à le comprendre.
Hum, non cela ne me dit rien. Je t'avoue que je ne vois pas pourquoi tu penses à cela...
Re: Montrer qu'un polynôme B divise un polynôme A
thoralf8weblen a écrit:Donc
y^2^(k+1) + y^2^k + 1 =Q
Or si on prend la valeurou
pour X, on aura:
y^2^(k+1) + y^2^k + 1 = 0
Doncet
sont des racines de y^2^(k+1) + y^2^k + 1.
Je ne vois AUCUNE DÉMONSTRATION, uniquement des affirmations sans aucun argument probant. Pourquoi est-ce que
Il est bien entendu que je sais pourquoi. Et il n'y a dans ce que tu écris par le moindre début de commencement de ce pourquoi.
Penses-tu avoir démontré quelque part que
Re: Montrer qu'un polynôme B divise un polynôme A
Si je comprends bien, dire que les racines qui annulent 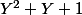 sont également des racines de X^2^(k+1) + X^k + 1, ce n'est pas viable comme raisonnement. Dans ce cas, je ne vois pas comment réaliser une démonstration de cela.
sont également des racines de X^2^(k+1) + X^k + 1, ce n'est pas viable comme raisonnement. Dans ce cas, je ne vois pas comment réaliser une démonstration de cela.
Si tu sais pourquoi, pourrais-tu peut-être m'aider ? Là, je pense que tourne en rond sans progresser sur mon problème de départ...
Je n'attends pas la réponse à mon problème. La réponse ne m'intéresse pas si je ne comprends pas le raisonnement qui amène à cette réponse. Je cherche à comprendre comment on arrive à la solution. Pour le moment, je ne vois rien de cela. Ce n'est pas faute de faire des efforts.
Si tu sais pourquoi, pourrais-tu peut-être m'aider ? Là, je pense que tourne en rond sans progresser sur mon problème de départ...
Je n'attends pas la réponse à mon problème. La réponse ne m'intéresse pas si je ne comprends pas le raisonnement qui amène à cette réponse. Je cherche à comprendre comment on arrive à la solution. Pour le moment, je ne vois rien de cela. Ce n'est pas faute de faire des efforts.
Re: Montrer qu'un polynôme B divise un polynôme A
thoralf8weblen a écrit:Si je comprends bien, dire que les racines qui annulentsont également des racines de X^2^(k+1) + X^k + 1, ce n'est pas viable comme raisonnement. .
Bien sûr que si. Mais tu n'as jamais donné d'argument pour justifier
Pourquoi t'obstines-tu à ne pas comprendre que c'est ce qui manque ?
Indication : pour démontrer que
Re: Montrer qu'un polynôme B divise un polynôme A
Pourquoi ) ^2^(k+1) +
^2^(k+1) + ^2) + 1 = 0 ?
+ 1 = 0 ?
Car la décomposition de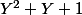 est
est (X - (-1 - i\sqrt{3})/2)
Quand on prend) ,
, (X - (-1 - i\sqrt{3}/2)) = 0.
= 0.
Comme X^2^(k+1) + X^2^k + 1 =(X - (-1 - i\sqrt{3}/2)Q)
Avec X =) , X^2^(k+1) + X^2^k + 1 = 0.
, X^2^(k+1) + X^2^k + 1 = 0.
Voilà mon raisonnement.
Car la décomposition de
Quand on prend
Comme X^2^(k+1) + X^2^k + 1 =
Avec X =
Voilà mon raisonnement.
Re: Montrer qu'un polynôme B divise un polynôme A
thoralf8weblen a écrit:Comme X^2^(k+1) + X^2^k + 1 =
Pourquoi ?
Re: Montrer qu'un polynôme B divise un polynôme A
Non je n'ai jamais vu cette notation. Je connais Un = {exp(2k )/n), k appartenant à Z}
)/n), k appartenant à Z}
Re: Montrer qu'un polynôme B divise un polynôme A
thoralf8weblen a écrit:Parce que
Et pourquoi est-ce que ça entraînerait que
N'utiliserais tu pas que
Re: Montrer qu'un polynôme B divise un polynôme A
Asse naïvement peut-être, je te répondrai qu'il s'agit simplement de remplacer 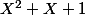 par la décomposition correspondante.
par la décomposition correspondante.
Hum... Je suis bien parti de la division X^2^(k+1) + X^k + 1 =Q) Mon erreur semble bien venir de là...
Mon erreur semble bien venir de là...
Hum... Je suis bien parti de la division X^2^(k+1) + X^k + 1 =
Re: Montrer qu'un polynôme B divise un polynôme A
Ouf ! Je pense que tu as compris maintenant pourquoi tu n'as fait aucune démonstration jusqu'à présent. Alors je répète mon
GaBuZoMeu a écrit:Indication : pour démontrer queest racine de
, il peut être utile de réaliser que le nombre complexe
est une racine cubique de l'unité.
60 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
