J'ai bien noté ton indication mais quand je remplace, je suis toujours embêté par le même point: traiter les puissances de puissances.
Montrer qu'un polynôme B divise un polynôme A
60 messages
- Page 2 sur 3 - 1, 2, 3
Re: Montrer qu'un polynôme B divise un polynôme A
Oui je comprends. J'aurai donc dû écrire "si 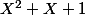 divise...".
divise...".
J'ai bien noté ton indication mais quand je remplace, je suis toujours embêté par le même point: traiter les puissances de puissances.
J'ai bien noté ton indication mais quand je remplace, je suis toujours embêté par le même point: traiter les puissances de puissances.
Re: Montrer qu'un polynôme B divise un polynôme A
1°) Quelles sont les racines cubiques de l'unité dans 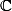 ?
?
Je pose comme d'habitude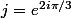 .
.
2°) Est-ce que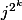 est une racine cubique de l'unité ? A-t-on
est une racine cubique de l'unité ? A-t-on 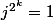 ?
?
Je pose comme d'habitude
2°) Est-ce que
Re: Montrer qu'un polynôme B divise un polynôme A
un peu de cours...
on a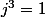
pour calculer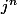 , on effectue la division euclidienne de l'exposant n par 3
, on effectue la division euclidienne de l'exposant n par 3
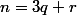
d'où
^q . j^r=1^q. j^r=j^r) r pouvant prendre les valeurs 0;1;2
r pouvant prendre les valeurs 0;1;2
pour conclure:
pour calculer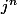 , on peut remplacer n par son résidu modulo 3. Une autre façon de le dire,
, on peut remplacer n par son résidu modulo 3. Une autre façon de le dire,
pour calculer les puissances de et de
et de , on peut calculer l'exposant modulo 3
, on peut calculer l'exposant modulo 3
Polynômes
Si X est une indéterminée, on a
^2=X^{2^k . 2}=X^{2^{k+1}})
on a
pour calculer
d'où
pour conclure:
pour calculer
pour calculer les puissances de
Polynômes
Si X est une indéterminée, on a
Re: Montrer qu'un polynôme B divise un polynôme A
Les racines cubiques de l'unité sont de la forme exp((i2 )/2).
)/2).
Oui j^2^k est racine cubique de l'unité.
Je le démontre comme cela: j^2^k = exp(i2 /3)^2^k
/3)^2^k
= exp(i4 /3)
/3)
= exp(i k)^(4/3)
k)^(4/3)
= 1^(4/3)
= 1
Mathelot, j'ai plusieurs questions:
1) Pourquoi r devrait valoir soit 0, soit 1 soit 2 ?
2) Je comprends bien ton rappel de cours mais quel est le lien avec mon problème de départ ? Je peine à le voir...
Oui j^2^k est racine cubique de l'unité.
Je le démontre comme cela: j^2^k = exp(i2
= exp(i4
= exp(i
= 1^(4/3)
= 1
Mathelot, j'ai plusieurs questions:
1) Pourquoi r devrait valoir soit 0, soit 1 soit 2 ?
2) Je comprends bien ton rappel de cours mais quel est le lien avec mon problème de départ ? Je peine à le voir...
Re: Montrer qu'un polynôme B divise un polynôme A
thoralf8weblen a écrit:1) Pourquoi r devrait valoir soit 0, soit 1 soit 2 ?
r est le reste de la division de n par 3. Il vaut donc 0;1 ou 2
thoralf8weblen a écrit:Oui j^2^k est racine cubique de l'unité.
preuve:
en effet , avec le calcul des puissances
Modifié en dernier par mathelot le 10 Jan 2021, 18:14, modifié 1 fois.
Re: Montrer qu'un polynôme B divise un polynôme A
Je te remercie. Mais par contre, je peine toujours à avancer sur mon problème de départ.
Il faut que je montre que/2) est racine de X^k^n + X^k + 1.
est racine de X^k^n + X^k + 1.
Je reste bloqué sur ce point.
Si je parviens à faire cela, je pourrai démontrer que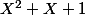 divise X^k^n + X^k + 1. Mais je ne vois toujours pas pourquoi Pn diviserait Pm...
divise X^k^n + X^k + 1. Mais je ne vois toujours pas pourquoi Pn diviserait Pm...
Il faut que je montre que
Je reste bloqué sur ce point.
Si je parviens à faire cela, je pourrai démontrer que
Re: Montrer qu'un polynôme B divise un polynôme A
On va étudier les puissances de j,c-a-d, 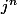
On a vu que l'on pouvait calculer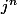 en réduisant l'exposant n modulo 3.
en réduisant l'exposant n modulo 3.
(est ce que tu connais les congruences ?)
complète le tableau
on calcule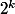 modulo 3
modulo 3

On a vu que l'on pouvait calculer
(est ce que tu connais les congruences ?)
complète le tableau
on calcule
Re: Montrer qu'un polynôme B divise un polynôme A
Oui je connais les congruences.
J'ai donc posé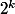 modulo 3 c-à-d:
modulo 3 c-à-d:
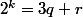 avec q > r
avec q > r
Donc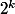 modulo 3 donne dans le tableau suivant:
modulo 3 donne dans le tableau suivant:


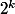

J'ai donc posé
Donc
Re: Montrer qu'un polynôme B divise un polynôme A
thoralf8weblen a écrit:Oui je connais les congruences.
J'ai donc posémodulo 3 c-à-d:
avec 3 > r >=0
Doncmodulo 3 donne dans le tableau suivant:

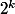
c'est très bien !! bravo
si k est pair,
d'où, qu'est ce que cela donne pour k impair ?
Re: Montrer qu'un polynôme B divise un polynôme A
Je vois bien que le reste est de 2 ! Mais je t'avoue ne pas voir où cela va m'amener...
Re: Montrer qu'un polynôme B divise un polynôme A
mathelot a écrit:
si k est pair,
d'où, qu'est ce que cela donne pour k impair ?
si k est impair,
Re: Montrer qu'un polynôme B divise un polynôme A
On appelle 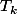 le polynôme
le polynôme
=Y^{2^{k+1}}+Y^{2^{k}}+1)
si k est pair, que vaut) ? (réponse demandée avec des j)
? (réponse demandée avec des j)
si k est pair, que vaut
Re: Montrer qu'un polynôme B divise un polynôme A
Je vois le lien maintenant.
Si k est pair, on a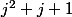
Si k est impair, on a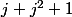
Reste à montrer que dans les deux cas, la somme est nulle, non ?
Si k est pair, on a
Si k est impair, on a
Reste à montrer que dans les deux cas, la somme est nulle, non ?
Re: Montrer qu'un polynôme B divise un polynôme A
thoralf8weblen a écrit:Je vois le lien maintenant.
Si k est pair, on a
Si k est impair, on a
Reste à montrer que dans les deux cas, la somme est nulle, non ?
oui, si tu veux
Re: Montrer qu'un polynôme B divise un polynôme A
thoralf8weblen a écrit:Je vois le lien maintenant.
Si k est pair, on a
Si k est impair, on a
Reste à montrer que dans les deux cas, la somme est nulle, non ?
avec la notation j
les trois termes sont en progression géométrique de raison j et de premier terme 1; d'où:
sinon avec j=-1/2+i rac(3)/2 tu peux faire le calcul.
Re: Montrer qu'un polynôme B divise un polynôme A
Ca marche !
Mais quel est le rapport avec l'énoncé de départ ? Je me suis un peu perdu en cours de route. En gros, on avait jusqu'ici n = 1 et m = k+1. Il suffirait d'avoir le même raisonnement en changeant les valeurs de n et m pour montrer que Pn divise Pm ?
Mais quel est le rapport avec l'énoncé de départ ? Je me suis un peu perdu en cours de route. En gros, on avait jusqu'ici n = 1 et m = k+1. Il suffirait d'avoir le même raisonnement en changeant les valeurs de n et m pour montrer que Pn divise Pm ?
Re: Montrer qu'un polynôme B divise un polynôme A
Je conclus la 1ère étape:
en résumé, quelque soit k entier naturel, j est racine de=Y^{2^{k+1}}+Y^{2^{k}}+1)
Comme le polynôme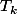 est à coefficients réels, et que
est à coefficients réels, et que  est le conjugué de j
est le conjugué de j
alors si j est racine de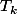 ,
,  son conjugué est également racine de
son conjugué est également racine de 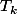
d'où
comme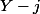 et
et 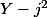 sont premiers entre eux,
sont premiers entre eux,
(Y-j^2) =Y^2+Y+1) divise
divise 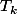
en résumé, quelque soit k entier naturel, j est racine de
Comme le polynôme
alors si j est racine de
d'où
comme
Modifié en dernier par mathelot le 11 Jan 2021, 18:34, modifié 2 fois.
Re: Montrer qu'un polynôme B divise un polynôme A
Pour conclure la question, il faut retrouver l'idée initiale de GBZM.. je réfléchis 

Re: Montrer qu'un polynôme B divise un polynôme A
Ne serait-ce pas à thoralf8weblen de réfléchir ?
Rappel :^b=X^{ab}) (ne pas confondre
(ne pas confondre ^b) avec
avec 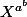 ).
).
Aussi :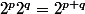 .
.
Rappel :
Aussi :
Re: Montrer qu'un polynôme B divise un polynôme A
remarque:
=Y^{2^{k+1}}+Y^{2^k}+1) est de la forme
est de la forme 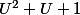 avec
avec 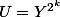
on a une progression géométrique:
d'où
=\dfrac{1-(Y^{2^k})^3}{1-Y^{2^k}}=\dfrac{1-(Y^3 )^{2^k}}{1-Y^{2^k}})
avec cette formule, on obtient que j et j^2 sont racines de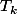
une formule
on a:
pour=T_n(Y^{2^{m-n}}))
on a une progression géométrique:
d'où
avec cette formule, on obtient que j et j^2 sont racines de
une formule
on a:
pour
60 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
