Matrices nilpotentes qui commutent
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 13 Juin 2009, 14:12
par J-R » 13 Juin 2009, 14:12
bonjour,
juste des pistes pour :
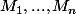
des matrices nilpotentes et commutant deux à deux.
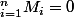
merci
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 13 Juin 2009, 14:48
par Nightmare » 13 Juin 2009, 14:48
Salut :happy3:
Une récurrence semble faire l'affaire.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 13 Juin 2009, 14:51
par Joker62 » 13 Juin 2009, 14:51
M1 = M2 =
0 1 1 1
0 0 1 1
0 0 0 1
0 0 0 0
Nilpotente d'ordre 4, M1 et M2 commutent et M1.M2 != 0
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 13 Juin 2009, 14:53
par Nightmare » 13 Juin 2009, 14:53
Oui il faut préciser que ce sont des matrices d'ordre n, indice final de la somme.
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 13 Juin 2009, 15:19
par Maxmau » 13 Juin 2009, 15:19
Bj
Je crois que le format des matrices est nxn
Comme les matrices commutent, elles doivent être simultanément trigonalisables.
Tu peux donc te ramener au cas où toutes ces matrices sont triangulaires à diagonale nulle.
Tu appliques alors le produit de matrices à une colonne X
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 14 Juin 2009, 09:49
par J-R » 14 Juin 2009, 09:49
re,
benh c'était un exo (il restait 5 min) de colle donc je m'en souvenais en gros...
(((Maxmau : j'ai pas encore de théorie sur la diagonalisation ...)))
mais sinon c'est résolut j'ai pu tirer un exo qui permettait d'arriver au résultat.
merci
@+
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 14 Juin 2009, 17:02
par yos » 14 Juin 2009, 17:02
On a, quelles que soient les matrices
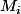
,
\leq rg(M_2...M_n\leq...\leq rg(M_n))
;
mais ici toutes les inégalités sont strictes, sinon l'une des matrices
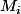
induirait un iso sur
)
(espace
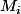
-stable car
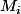
commute avec
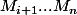
) ce qui n'est pas compatible avec la nilpotence de
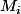
.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 14 Juin 2009, 22:23
par Joker62 » 14 Juin 2009, 22:23
Elle sort d'où cette inégalité sur le rang ?
Je sais bien que rg(AB) <= Min(rg(A),rg(B))
Mais j'vois pas comment tu parviens à celle-ci :/
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Juin 2009, 23:04
par Nightmare » 14 Juin 2009, 23:04
En particulier,
\le rg(A)\;et\; rg(AB)\le rg(B))
:lol3:
Donc
)\le rg(M_{2}...M_{n}))
etc.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 14 Juin 2009, 23:17
par Joker62 » 14 Juin 2009, 23:17
Lol !
La honte :D
Désolé d'avoir posté pour ça...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
des matrices nilpotentes et commutant deux à deux.
des matrices nilpotentes et commutant deux à deux.