Projecteurs et symetries qui commutent avec un endom diago

[Don vito]

Salut!
Soit U un endomorphisme diagonalisable .
Sachant qu'un endomorphisme v commute avec u ssi v stabilise les ss espaces propres de u.A quelle condition un projecteur commute avec u, même question pour une symétrie?

j'ai un peu pensé , mais je ne suis pas sûr , je crois que pour les projections ya que l'identité??

[arnaud32]

si tu te places ds une base de diagonalisation. (e1, ..., en)
que penses tu des projecteurs sur ei suivant vect (ek, k different de i)?

[barbu23]

Bonjour à tous,

J'ai un gros trou de mémoire :

Quelles sont les matrices correspondantes aux endomorphismes , représentant une symétrie ou un projecteur ?
Pour un projecteur, je pense que c'est avec , et , avec : , n'est ce pas ?

Merci d'avance. :happy3:

[wserdx]

Si les projecteurs sont caractérisés par et les symétries par
les valeurs propres sont 0 et 1 pour les projecteurs et 1 et -1 pour les symétries.
On doit donc avoir ou
et ou

[barbu23]

Donc, la matrice d'une symétrie est , à position des vecteurs colonnes près. n'est ce pas ?

[Don vito]

Merci arnaud32 d'avoir répondu et je m'excuses en même temps pour mon retard,
sinon il me parait que la famille de projecteur que tu as définit (p1,...pn) génère les projecteurs de E, autrement dit tout projecteur p appartient à vect(p1,...pn).Donc pour que p commute avec u , il faut que chaque pi commute avec u.Ce qui n'est possible(d’après vérification sur matrices correspo) que lorsque u est diagonal.
Serait bien la réponse , j'ai l'impression de m’être trop précipité dans le raisonnement??

[wserdx]

Les sous-espaces propres de u ne sont pas nécessairement de dimension 1 (sauf si c'est une hypothèse de ton problème).
Pour que p projecteur commute avec u il faut et il suffit que la restriction de p à chaque sous-espace propre de u soit elle-même un projecteur. Idem pour les symétries.
La caractérisation des projecteurs et des symétries est si je ne me trompe et 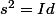, sauf cas particuliers, ils ne forment pas de groupes ni même d'espaces vectoriels.

[Don vito]

ok, Merci Wserdx !Mais pourrai je savoir le lien avec la dimension 1 (je comprends que c'est en réponse à ce que j'ai dit , j'ai sans doute dit quelque chose sans m'en rendre compte.)
Sinon pourrais tu aussi m'expliciter d'avantage la réponse pourquoi justement la restriction...etc
pour te dire ce qui me colle à la tête( comment j’imagines) , je vois que cette restriction est la projection sur chacun des sous espaces propres parallèlement à la somme directes de tous les autres...ce qui n'est pas toujours vrai je crois.

Merci de bien vouloir m'aider.

[wserdx]

Si tous les sous espaces propres sont de dimension 1, c'est que les valeurs propres sont distinctes et d'ordre de multiplicité 1. Il y a alors une unique base de diagonalisation (à l'ordre près des vecteurs).
Dans ce cas on doit avoir pour tout vecteur propre ou . On peut donc même dire qu'il y a exactement projecteurs qui commutent avec (si est la dimension de l'espace)
Dans le cas où un sous espace propre est de dimension supérieure à 1, la restriction de à ce sous espace est où est la valeur propre et donc toute base de ce sous espace diagonalise la restriction. Tout projecteur de ce sous espace convient alors.
On reconstruit le projecteur final à partir de la décomposition en somme directe des sous-espaces propres.