Matrice d'un produit scalaire ?

par **capitaine nuggets** » 03 Mar 2013, 17:58

Bonjour, j'aurais besoin de votre aide pour savoir si la matrice

est la matrice d'un produit scalaire.
La matrice

étant symétrique, c'est bien parti, mais je ne sais pas si ça suffit...

Peut-on expliciter ce produit scalaire ?
Si oui, est-il unique ?

Merci d'avance :++:

par **vincentroumezy** » 03 Mar 2013, 18:04

Salut !
Un produit scalaire est défini positif.
Tu pourrais tenter d'étudier le spectre de ta matrice.

par **capitaine nuggets** » 03 Mar 2013, 18:17

vincentroumezy a écrit:Salut !
Un produit scalaire est défini positif.
Tu pourrais tenter d'étudier le spectre de ta matrice.

Heu ... pourquoi étudier le spectre de la matrice ?
Je ne vois pas le lien avec le fait qu'un produit scalaire est défini positif...

Le polynôme caractéristique associé à

étant

, le spectre de

est

.

par **capitaine nuggets** » 03 Mar 2013, 18:27

vincentroumezy a écrit:Salut !
Un produit scalaire est défini positif.
Tu pourrais tenter d'étudier le spectre de ta matrice.

Heu ... pourquoi étudier le spectre de la matrice ?
Je ne vois pas le lien avec le fait qu'un produit scalaire est défini positif...

Le polynôme caractéristique associé à

étant

, le spectre de

est

.

par **Wenneguen** » 03 Mar 2013, 18:28

capitaine nuggets a écrit:Heu ... pourquoi étudier le spectre de la matrice ?
Je ne vois pas le lien avec le fait qu'un produit scalaire est défini positif...

Le polynôme caractéristique associé à étant , le spectre de est .

Une matrice est définie-positive si et seulement si ses valeurs propres sont strictement positives :happy2:

par **Nightmare** » 03 Mar 2013, 18:29

Une matrice symétrique est définie positive si et seulement si ses valeurs propres sont strictement positives, c'est le cas ici.

par **capitaine nuggets** » 03 Mar 2013, 18:32

Ah d'accord, je ne savais pas.

Donc pour montrer que A est bien la matrice d'un produit scalaire il faut, et il suffit qu'elle soit symétrique et que toutes ces valeurs propres soient positives strictement ?

Peut-on expliciter ce produit scalaire ?

par **Nightmare** » 03 Mar 2013, 18:34

Oui : =txAy est le produit scalaire recherché.

par **capitaine nuggets** » 03 Mar 2013, 18:37

Nightmare a écrit:Oui : =txAy est le produit scalaire recherché.

Et comment fais-tu pour le trouver ?

par **Nightmare** » 03 Mar 2013, 18:38

C'est-à-dire?

par **capitaine nuggets** » 03 Mar 2013, 18:45

Nightmare a écrit:C'est-à-dire?

Ben comment as-tu fait pour savoir que le produit scalaire associé à A est txAy ?

par **Wenneguen** » 03 Mar 2013, 21:01

La matrice dans une base

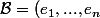associée à une forme bilinéaire symétrique

est définie comme la matrice carrée de coefficient général

.
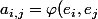Après

(avec X et Y les vecteurs coordonnées de x et y dans la même base

c'est une égalité connue que je pense que tu n'as pas à redémontrer (ça se fait en développant les deux membres avec des x et y décomposés dans la base, et en remarquant qu'ils sont égaux) :we:

par **lionel52** » 03 Mar 2013, 22:16

Sinon la forme quadratique associée est :

f(x,y,z) = 4x² + 4y² + 4z² + 2xy + 2xz + 2yz = (x+y+z)² + 3x² + 3y² + 3z² >= 0 avec égalité ssi x,y et z sont nuls

Matrice d'un produit scalaire ?

Matrice d'un produit scalaire ?

Qui est en ligne