Bonjour,
Il
Maths injection et surjection
5 messages
- Page 1 sur 1
Re: Maths injection et surjection
Si quelqu’un pouvait m’aider ce serait vraiment sympa.
@sara4 a effacé sa question. Elle se demandait à quelles conditions la fonction g, définie de R-{1} dans R
Bonsoir,
soit
Pour obtenir
si on peut calculer x fonction de y, ceci prouve qu'il existe un et un seul antécédent de y
et donc que la restriction de g à R-{1} est bijective (évidemment en précisant les domaines de départ et d'arrivée et en restreignant le domaine d'arrivée de g)
si tu calcules la fonction f, réciproque de g, une surprise t'attend (!)
De plus, lors du calcul de x, il y a une restriction sur y qui apparait, ce qui permet de définir le domaine de définition de f.
Modifié en dernier par mathelot le 09 Jan 2021, 13:02, modifié 8 fois.
Re: Maths injection et surjection
Soient x et y deux réels différents de 1. 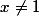 et
et 
si on pose
) (*)
(*)
alors y est l'image de x par la fonction g et x est un antécédent de y , toujours par la fonction g.
on va calculer x fonction de y
y(x-1)=x+1
yx - x =y+1
x(y-1)=y+1
là, il faut supposer y différent de 1
 (**)
(**)
conclusion:
Les réels y différents de 1 ont un antécédent.
g , restreinte au codomaine R-{1} est surjective. (le codomaine est l'espace d'arrivée de g)
L'antécédent x calculé est unique. Donc g est injective.
finalement, g est une bijection de R-{1} sur R-{1}
soit f la bijection réciproque de g. x=f(y)
=\dfrac{y+1}{y-1}) d'après (**)
d'après (**)
la surprise est que f=g
si on pose
alors y est l'image de x par la fonction g et x est un antécédent de y , toujours par la fonction g.
on va calculer x fonction de y
y(x-1)=x+1
yx - x =y+1
x(y-1)=y+1
là, il faut supposer y différent de 1
conclusion:
Les réels y différents de 1 ont un antécédent.
g , restreinte au codomaine R-{1} est surjective. (le codomaine est l'espace d'arrivée de g)
L'antécédent x calculé est unique. Donc g est injective.
finalement, g est une bijection de R-{1} sur R-{1}
soit f la bijection réciproque de g. x=f(y)
la surprise est que f=g
Modifié en dernier par mathelot le 09 Jan 2021, 13:08, modifié 3 fois.
Re: Maths injection et surjection
Bonsoir
au moins le 3e site pour la même demande...que c'est pénible...
au moins le 3e site pour la même demande...que c'est pénible...
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Maths injection et surjection
autres méthodes
soient et
et  deux réels différents de 1.
deux réels différents de 1.

soit par produit en croix
(x_2-1)=(x_2+1)(x_1-1))



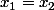
La fonction g est donc injective.
L'examen du tableau de variation de g montre que g est une surjection , de R-{1} sur R-{1}
soient
soit par produit en croix
La fonction g est donc injective.
L'examen du tableau de variation de g montre que g est une surjection , de R-{1} sur R-{1}
Modifié en dernier par mathelot le 09 Jan 2021, 12:45, modifié 1 fois.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
