Manipulation de nombres réels
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
foulosophe
- Messages: 1
- Enregistré le: 08 Oct 2010, 14:03
-
 par foulosophe » 08 Oct 2010, 14:05
par foulosophe » 08 Oct 2010, 14:05
Bonsoir à tout le monde,
J'ai un petit exercice que j'essaie de résoudre, mais je bloque ! J'ai jamais été excellent en math et là je me rend compte que c'est plus trop les cours lycée qu'on fait...
Voilà l'énoncé
- Code: Tout sélectionner
1/ Soit x,y,z nombres réels. Montrer que l'on a x²+y² >(ou égal) 2xy
En déduire l'inégalité : x²+y²+z² >(ou égal) xy + yz+ zx
2/ Montrer que l'on a (x+y)² >(ou égal) 4xy
En déduire que si x,y,z sont positifs ou nuls, alors on a :
(x+y)(y+z)(z+x) >(ou égal) 8xyz
Si vous pouviez me donner quelques pistes de résolution par ce que je reste sec devant la feuille !
Merci à vous. Bonne après-midi..

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 08 Oct 2010, 14:41
par Ericovitchi » 08 Oct 2010, 14:41
Déjà x²+y² >= 2xy fais passer le 2xy de l'autre coté et reconnais une identité remarquable
Pour x²+y²+z² >= xy + yz+ zx Tu pars du membre de droite, et tu te sers de ce que tu as déjà démontré pour majorer xy, yz et zx (donc par (x²+y²)/2, etc... )
(x+y)² >= 4xy tu développes à gauche, tu fais passer le 4xy à gauche, tu simplifies et tu tombes sur une identité remarquable qui rends l'inégalité évidente
Essayes de trouver la dernière tout seul
-
lexabirot
- Messages: 1
- Enregistré le: 08 Oct 2010, 14:38
-
 par lexabirot » 08 Oct 2010, 14:41
par lexabirot » 08 Oct 2010, 14:41
email:
lexabirot@yahoo.fr portable: 0607080910
foulosophe a écrit:Bonsoir à tout le monde,
J'ai un petit exercice que j'essaie de résoudre, mais je bloque ! J'ai jamais été excellent en math et là je me rend compte que c'est plus trop les cours lycée qu'on fait...
Voilà l'énoncé
- Code: Tout sélectionner
1/ Soit x,y,z nombres réels. Montrer que l'on a x²+y² >(ou égal) 2xy
En déduire l'inégalité : x²+y²+z² >(ou égal) xy + yz+ zx
2/ Montrer que l'on a (x+y)² >(ou égal) 4xy
En déduire que si x,y,z sont positifs ou nuls, alors on a :
(x+y)(y+z)(z+x) >(ou égal) 8xyz
Si vous pouviez me donner quelques pistes de résolution par ce que je reste sec devant la feuille !
Merci à vous. Bonne après-midi..
-
hazaki
- Membre Naturel
- Messages: 70
- Enregistré le: 05 Oct 2010, 20:31
-
 par hazaki » 09 Oct 2010, 18:58
par hazaki » 09 Oct 2010, 18:58
Bonjour, je suis confronté au même exercice, le début est évident mais je suis bloqué à la dernière question,
j'en suis au moment où je dois prouver que yx² + xz² + zx² + zy² + xy² + yz² 6xyz.
Merci de bien vouloir m'aider

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 09 Oct 2010, 19:17
par Ericovitchi » 09 Oct 2010, 19:17
(x+y)(y+z)(z+x) >= 8xyz ça ? (car ça n'est pas ce que tu as écris)
tu as montré à la question d'avant que (x+y)² >= 4xy donc que (x+y)>= 2
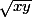
donc (x+y)(y+z)(z+x) >=
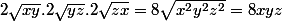
-
hazaki
- Membre Naturel
- Messages: 70
- Enregistré le: 05 Oct 2010, 20:31
-
 par hazaki » 09 Oct 2010, 19:30
par hazaki » 09 Oct 2010, 19:30
Bonjour,
Merci de ta réponse,
pour ma part, j'avais développé et je n'arrivais à rien donc merci de l'aide et bonne soirée.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
