J'ai un petit prog à faire où je dois manipuler des matrices .
Malheureusement je n'en ai jamais fais avant. Je me tourne vers vous car mon probleme est purement theorique et je sais que si je comprend comme ça fonctionne je pourrais faire un algo donc voila.
Je dois pouvoir manipulation une matrice identité 2D avec des translation par un vecteur x,y , une homothétie de rapport i suivant Oi et j suivant Oj, une rotation par un angle i et une symetrie par rapport a un axe inclinée d'angle n.
Nous partons d'une matrice identité en 2D
J'ai cherché sur le net pour ces transformation (je n'avais jamais vu les matrices auparavant)
Pour une translation :
Si on part d'une matrice identité alors la translation sera :
[1 0 Tx]
[0 1 Ty]
[0 0 1 ] donc si je veux faire une translation de vecteur 2,3 j'aurais :
[1 0 2]
[0 1 3]
[0 0 1] confirmation?
Pour une homothetie :
J'avoue avoir vraiment pas compris cette partie
Pour une rotation d'angle i :
J'ai crus comprendre qu'il fallait utilisé cette formule :
[cos(i) -sin(i) 0]
[sin(i) cos(i) 0]
[ 0 0 1]
Pour une symetrie par un axe inclinée d'angle n :
Je sais que : x = cos(n)²-sin(n)²
y = 2*cos(n)*sin(n)
Mais je ne sais pas où les places dans ma matrice sauf pour le x :
[x 0 0]
[0 1 0]
[0 0 1] mais sinon le y je ne sais pas, pareil... est ce juste un 'remplacement' ou une addition/multiplication ... ?
Je possède des exemples pour chaque transformation avec evidemment que les reponses mais pas l'explication du pourquoi du comment ... à chaque fois j'arrive plus ou moins à trouver mais bon cela reste néanmoins flou (exemple pour la symetrie ou n = 270).
[-1 0 0]
[0 1 0]
[0 0 1] en calculaant je trouve x = -1 et y = 0. donc ok pour x mais pour y ?
Déjà de base j'ai du mal mais là où ça se complique c'est lorsque qu'il faut faire l'un après l'autre par exemple une Rotation puis une Symetrie est ce qu'il faut faire Matrice_RESULTAT = R . S où je ferrais le produit comme cela :
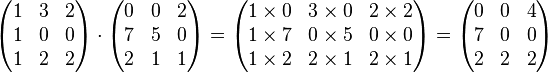
je vous donne l'exemple que j'ai pour ce cas où rotation d'angle 37 et symetrie d'angle 69:
[-0,191 0,982 0]
[ 0,929 0,191 0]
[ 0 0 1] je n'arrive pas à trouver ce resultat
Bref j'ai retourné le sujet dans tout les sens, cherché sur wiki, plein de site qui parle de matrice et je tourne en rond, je n'ai pas de prof de maths pour m'aider donc vous comprenez bien que c'est un peu difficile.
A la fin je dois etre capable de faire faire à ma matrice une translation, homothetie, une rotation et une symetrie. M_Resulat = T.H.R.S ???
Merci d'avoir pris le temp de lire et j'espère que quelqu'un sera apte à me répondre sur ce forum.
Amicalement
ksta
