Loi uniforme (again)

[fatal_error]

Cette problématique de répartition uniforme a déjà été évoquée. Je me souviens avoir dit que c'est pas évident, et d'ailleurs, de mémoire, Sylviel avait confirmé. C'était il n'y a pas très longtemps, mais je ne souviens plus où.

non tu n'as rien dit du tout. Ou alors j'ai rate quelquechose.

Ma question etait: Quelle courbe obtiens tu en lancant 50 fois une piece en mettant en ordonnee le nombre de pil et de face obtenues.

Tu n'as pas plus commente ici la courbe de mathusalem. Qu'en penses-tu, est-elle fausse?

[Dlzlogic]

J'essaye juste de rester terre à terre.
- Dans une série d'expérience, la répartition des écarts à la moyenne suit-elle la loi normale OUI-NON ?
Le terme expérience est à prendre dans son sens le plus général, mathématique, aléatoire, équiprobable. Si le dé est pipé, on appelle ça "écart systématique". L'examen des résultats permet de le détecter : décalage de l'axe.
- Dans la formule d'écart-type et dans la méthode des moindres carrés l'utilisation des valeurs (mesures ou écarts) au carré résulte-t-elle de l'habitude, de s'assurer que c'est positif ou au contraire cela résulte-t-il directement et impérativement de la loi normale OUI-NON ?
- La combinaison des écarts accidentels se fait par addition ou quadratiquement OUI-NON ?
- Si on veut étudier une situation d'après une répartition uniforme dans un espace limité, disons un carré, l'utilisation d'un générateur de nombre aléatoire type rand() X et Y indépendants, convient-elle OUI-NON ?

Si j'oublie des cas où j'ai "voulu l'utiliser", on voudra bien me le préciser.

Juste un mot sur l'exemple de la pluie.
On admet généralement que des réseaux d'assainissement pluvial doivent garantir une évacuation dans débordement pour des périodes décennales. (Les choses sont un peu plus compliquées mais gardons ces hypothèses pour l'exemple actuel).
Est-ce que ça signifie qu'on est tranquille pendant 10 ans ? Réponse : NON.
Est-ce que ça signifie que si ça déborde l'année suivante le bureau d'étude s'est trompé ? Réponse : NON.
Est-ce que ça signifie que si de mémoire d'homme le réseau n'a jamais été insuffisant, le bureau d'étude s'est trompé ? Réponse : OUI.

Par contre, cela signifie que chaque année, sur le terriroire français, une certaine proportion des réseaux sera insuffisant et qu'il y aura une certaine proportion d'inondations.

Concernant la loi de Cauchy, désolé, je ne sais pas ce qu'elle représente. La seule chose que je connaisse en la matière est la relation entre des évènement aléatoires, donc qui suivent une loi uniforme, et la répartition suivant la loi normale, courbe de Gauss. Pour la loi de Cauchy, je ne demande qu'à m'informer.

[Dlzlogic]

non tu n'as rien dit du tout. Ou alors j'ai rate quelquechose.

Ma question etait: Quelle courbe obtiens tu en lancant 50 fois une piece en mettant en ordonnee le nombre de pil et de face obtenues.

Tu n'as pas plus commente ici la courbe de mathusalem. Qu'en penses-tu, est-elle fausse?

J'ai retrouvé ma simulation concernant la répartition sur un carré, voila le résultat, il s'agissait de distances entre villes, le fichier est daté du 25/01/2012.

Code: Tout sélectionner

 Etude des positions X
Nombre = 100  MoyenneX = 0.25  emqX=30.76  epX=20.51
Classe 1  nb=   0  0.00%  théorique 0.35%
Classe 2  nb=   0  0.00%  théorique 2%
Classe 3  nb=  14  14.00%  théorique 7%
Classe 4  nb=  15  15.00%  théorique 16%
Classe 5  nb=  23  23.00%  théorique 25%
Classe 6  nb=  14  14.00%  théorique 25%
Classe 7  nb=  21  21.00%  théorique 16%
Classe 8  nb=  13  13.00%  théorique 7%
Classe 9  nb=   0  0.00%  théorique 2%
Classe 10 nb=   0  0.00%  théorique 0.35%
 Etude des positions Y
Nombre = 100  MoyenneY = 249.74  emqY=28.16  epY=18.77
Classe 1  nb=   0  0.00%  théorique 0.35%
Classe 2  nb=   0  0.00%  théorique 2%
Classe 3  nb=  13  13.00%  théorique 7%
Classe 4  nb=  16  16.00%  théorique 16%
Classe 5  nb=  17  17.00%  théorique 25%
Classe 6  nb=  24  24.00%  théorique 25%
Classe 7  nb=  21  21.00%  théorique 16%
Classe 8  nb=   9  9.00%  théorique 7%
Classe 9  nb=   0  0.00%  théorique 2%
Classe 10 nb=   0  0.00%  théorique 0.35%

Concernant les pièces pile ou face, il est bien évident qu'il y aura autant de pile que de face. Mais je retourne la question qui m'a été posée : "Comment la pièce se souvient-elle qu'elle doit rattraper (éventuellement) son retard de pile (resp. face) ?

Concernant les courbes de Mathusalem, je ne peux rien commenter, je ne sais pas comment elles ont été dessinées.

Ci-dessous, une citation partielle de cesar "28/04/2006". Titre de la discussion "Courbe de gauss".

Le test "bateau" dit du "khi2" (lettre grecque khi, indice 2) est une sorte de "bonne à tout faire", car c'est un test d'homogenité, d'independance et d'ajustement. C'est cette derniere propriété qui nous interesse ici. Il est helas delicat et fastidieux à appliquer, mais il est "robuste". C'est quasi impossible de vous expliquer toute la theorie ici, mais seulement des grandes lignes. Pour faire le test d'adéquation de la loi gaussienne, il faut d'abord diviser les échantillons en "classes" (pas en classes scolaire, il s'agit d'une partition d'un ensemble...). Ici vient la premiere difficulté : il faut faire un plus grand nombre de classes, tout en ayant des classes assez vastes, ce qui est contradictoire. en general, pour n>=200 on prend k classes = n/5 ...et on recommande de ne pas regrouper les classes extremes, meme si l'effectif est inferieur à 5, car un bon accord avec ces classes justifie l'ajustement... (boujour le travail "au pif"...)
ensuite, on determine le nombre de degrés de liberte (v= k -r -1), avec k, le nombre de classes, r le nombre de parametre (ici r=2, soit la moyenne et l'écart type...) et on calcule la valeur de la fonction Khi2. A partir de là, on fixe le seuil de confiance du test, en general, on prend un seuil Probabilité = 0.05 tel que le kh2 soit superieur à C-alpha. C-alpha est donné par les valeurs tabulées de khi2 (en fonction de v). C'est à dire qu'il y a 1-0.05 = 0.95 = 95% de probabilité que le khi2 soit inferieur à C-alpha. Si le khi2 est superieur à C-alpha, l'ajustement n'est pas bon et la gaussienne refusée, si il est en dessous, il est accepté et la loi gaussienne justifiée.

Pour mémoire, le test du Khi² est une méthode qui est une légère simplification (absence de calculateur à l'époque) de la méthode décrite dans ces différents fils. (écart probable 25% ; 16% ; 7% ; 2%).

[fatal_error]

- Dans une série d'expérience, la répartition des écarts à la moyenne suit-elle la loi normale OUI-NON ? Je ne sais pas
- Dans la formule d'écart-type et dans la méthode des moindres carrés l'utilisation des valeurs (mesures ou écarts) au carré résulte-t-elle de l'habitude, de s'assurer que c'est positif ou au contraire cela résulte-t-il directement et impérativement de la loi normale OUI-NON ? je ne sais pas
- La combinaison des écarts accidentels se fait par addition ou quadratiquement OUI-NON ? je ne sais pas
- Si on veut étudier une situation d'après une répartition uniforme dans un espace limité, disons un carré, l'utilisation d'un générateur de nombre aléatoire type rand() X et Y indépendants, convient-elle OUI-NON ? oui


edit: obsolete, cross post
Voila, jai repondu a tes questions. Que penses-tu des courbes de mathusalem? Que te donne ton experience de lancer de de suggeree dans mon precedent poste?

[fatal_error]

Concernant les pièces pile ou face, il est bien évident qu'il y aura autant de pile que de face. Mais je retourne la question qui m'a été posée : "Comment la pièce se souvient-elle qu'elle doit rattraper (éventuellement) son retard de pile (resp. face) ?

Je ne n'ai pas pose cette question.

Si tu lances un de, mettons 50 fois, es-tu d'accord que toutes les faces sortent a peu pres autant de fois?

[Dlzlogic]

Je ne n'ai pas pose cette question.

Si tu lances un de, mettons 50 fois, es-tu d'accord que toutes les faces sortent a peu pres autant de fois?

Oui naturellement (dés non pipés).
Mais on a besoin de plus d'information dans la réalité professionnelle.
Pour rester avec les dés on peut vérifier la répartition des écarts de nombre de sorties par rapport à la moyenne (= 50/6).
Doraki en bien voulu jouer le jeu, il a fait 20 tirages, et les résultats étaient tellement conformes à la théorie, malgré le faible nombre que je me souviens lu avoir "si je je ne savais pas que ça venait de toi, je pourrais supposer ..." ou qqch comme ça.
Petit exemple d'application (peut-être déjà cité).
Pour les travaux de mesure il existe des tolérances bien précises. Si les écarts ne respectent pas la répartition normale (ie courbe de Gauss), et pas seulement les écarts maximums, les travaux sont refusés.
Pour la question sur la mémoire, je sais que c'est pas toi, je crois Doraki, mais il est possible que ce fil ait disparu dans la tourmente de l'année dernière.

[fatal_error]

Mais on a besoin de plus d'information dans la réalité professionnelle.

J'en doute pas mais c'est pas ma question.

Es-tu d'accord qu'en tracant la courbe qui au numero de face du de associe le nombre de fois que le de est sorti que on a a peu pres une droite horizontale? (et donc pas une gaussienne?)

[Mathusalem]

T'es agaçant Dlzlogic. Tu balayes d'un revers de la main ce que j'ai fait en prétendant que j'essaie de prouver que j'ai raison par le graphe, plutôt que par le calcul. Mais c'est précisément la gueule différente des deux graphes qui devrait te faire tilter que l'un est issu d'un tirage uniforme, l'autre d'un tirage gaussien. J'ai même fait deux jolis dessins pour que tout le monde comprenne où tu te fourvoies.

Suite à la remarque de Doraki, j'ai changé d'algo et je t'ai fait un beau tirage complet.

On tire 10^6 fois un dé à 10^3 faces.
Résultats :



Maintenant, je zoome par exemple sur le tirage gaussien, et j'illustre le raisonnement de Dlzlogic



J'ai pris la face 487, et illustré la différence entre sa valeur simulée, et sa moyenne.

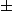
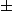
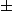
Sur tous les points considérés du tirage gaussien, l'écart maximal est de EMAX. Si tu subdivises EMAX en N intervalles, et que tu comptes combien de simulations sont dans 1 écart EMAX/N, 2EMAX/N, 3EMAX/N, etc... et que tu fais un plot du nombre de faces qui sont dans un écart, 2 écarts, etc.. tu vas obtenir un truc qui ressemble à du gaussien.



Là j'ai divisé en 34 l'écart max, et j'ai compté. La légende spécifie EMAX(tirage) parce qu'il est différent pour le gaussien et l'uniforme. [ EDIT : Je prend enfait Emax (qui est positif ou négatif) et je multiplie par 2 pour englober toutes les valeurs autour de la moyenne. Ca me fait un intervalle dont le milieu est environ la valeur moyenne. Ensuite je divise par N... ]

Et c'est ça que tu fais. Nous ce qu'on te dit, c'est de regarder le premier graphe, et réaliser qu'un des graphes est issu d'un tirage uniforme, l'autre d'un tirage normal. Toi, tu fais pas ça. T'as des chiffres, et tu vas tout de suite au graphe 3. Je crois que les graphes sont clairement expliqués. Tu peux les reproduire chez toi à plus petite échelle et faire les calculs que tu veux, tu verras que t'attéris sur le graphe 3 (qui d'ailleurs ici est assez pourri - faudrait augmenter le nombre de faces de dés pour que ça soit joli).

Au passage : j'évite de relever ton incompétence dans le domaine des calculs d'incertitude depuis une quinzaine de postes où toi tu essayes de provoquer. C'est pas très constructif de ta part.

[Dlzlogic]

Es-tu d'accord qu'en tracant la courbe qui au numero de face du de associe le nombre de fois que le de est sorti que on a a peu pres une droite horizontale? (et donc pas une gaussienne?)

Oui, ce qui signifie, en d'autres termes que le dé se souvient du nombre de fois que chaque face est sortie.

Donc, soit M la moyenne des nombres de tirages de chacune des faces. Dans le cas présent de dé, M est connu = N/6, si N est le nombre de tirages. M = Somme(ti)/6 : moyenne arithmétique.
Si on appelle e1 à e6 les écarts entre le nombre de sorties ti et M, et Ec (= écart-type) = sqrt(Somme(ei²)/6), et Ep(=écart probable) = Ec *2/3, alors
1- la somme des ei négatifs est égale à la somme des ei positifs
2- la répartition des ei est conforme à {25% ; 16% ; 7% ; 2%}
ces 8 classes correspondent à {1 Ep ; 2 Ep ; 3 Ep ; 4 Ep}, de chaque côté du zéro (ou plutôt de la moyenne arithmétique des écarts pour être rigoureux).
Il y a une cinquième classe qui contient 0.35% des écarts. Les valeurs situées dans cette classe sont habituellement considérés comme suspects, sauf si le nombre de tirages est très grand, c'est à dire si 7 pour 1000 a une signification.
Il est bien évident que le nombre des variables ei étant faible le terme "égal" est à prendre au sens "à peu près égal". On peut considérer que pour N > 20 "égal" pourra être pris au sens "presque égal".

Ceci a été observé et vérifié dans toute sorte d'environnements, de situations etc.
Les pourcentages et limites de classe indiqués correspondent à la loi normale, dont la courbe de Gauss est la représentation.
Bien entendu, les évènements doivent satisfaire aux conditions du hasard, c'est à dire une loi uniforme.

Pour mémoire
http://www.dlzlogic.com/Gauss.png

[beagle]

ben ça c'est joli !!!
Je parlais des images de Mathusalem.

p estimée que Dlzlogic botte en touche en faisant des écarts type ?

[fatal_error]

Oui

d'apres toi, la fonction rand de C++ (stdio/stdlib/math) je sais plus suit une loi uniforme, une loi normale, ou une loi on sait pas?

[Dlzlogic]

@ Mathusalem,
Puisque tu as raison, pourquoi continues-tu à correspondre ?
Pourquoi tu ne veux pas jouer le jeu pour me mettre en défaut : une liste de tirages (avec des chiffres) dans laquelle tu auras glissé des tirages "trafiqués".
D'ailleurs j'ai suffisamment souvent décrit la méthode pour que ceux qui ont lu la connaissent par coeur.
Tu ne m'as toujours pas dit comment tu appliques le théorème central limite.

J'ai retrouvé dernièrement des compte-rendus de travaux du cyclotron de Genève. Comme preuve de la qualité des opérations ils publient de très jolies courbes. Ca t'intéresse ?

[beagle]

et voilà une touche qui renvoie au-dela des 22 mètres,
belle action stéréotypée , mais quelle touche tout de mème!

[Dlzlogic]

d'apres toi, la fonction rand de C++ (stdio/stdlib/math) je sais plus suit une loi uniforme, une loi normale, ou une loi on sait pas?

La fonction rand() produit un nombre pseudo-aléatoire.
Il est "pseudo" parce qu'il y a un cycle de 4.10^9.
Donc on peut dire que le nombre sorti est aléatoire, c'est à dire que chaque nombre a autant de chances de sortir qu'un autre. C'est, je crois, ce qu'on appelle une loi uniforme.
Comme dit dans des réponses précédentes, des tirages aléatoires sortent avec des écarts à la moyenne qui respectent la loi normale.
A part me répéter, je ne vois pas ce que je peux répondre d'autre.

[fatal_error]

C'est, je crois, ce qu'on appelle une loi uniforme.

ok.

On prend un quadrillage avec les abscisses et ordonnées de 0 à 2 (un morpion quoi).
On dit que X représente le numéro d'une colonne du quadrillage.
Si X suit une loi uniforme, X a autant de chance de valoir 0; 1 ou 2.

Sommes nous d'accord?

[Dlzlogic]

ok.

On prend un quadrillage avec les abscisses et ordonnées de 0 à 2 (un morpion quoi).
On dit que X représente le numéro d'une colonne du quadrillage.
Si X suit une loi uniforme, X a autant de chance de valoir 0; 1 ou 2.

Sommes nous d'accord?

Je sais pas trop ce que tu essayes de me faire dire.
Prend la simulation sur les villes.
La sortie des X et celle des Y est aléatoire (rand() --> loi uniforme).
Considère les colonnes où la sortie des X est dans les classes à 25%.
Considère les cases des X sélectionnés et dont le Y est dans les classes 25%.
Maintenant, fais la même chose avec les classes 2%.
Le tirage est suivant une loi uniforme, mais crois-tu que les cases dans l'un et l'autre cas auront le même nombre de villes, ou un nombre presque équivalent ?

[fatal_error]

Je sais pas trop ce que tu essayes de me faire dire.
Prend la simulation sur les villes.
La sortie des X et celle des Y est aléatoire (rand() --> loi uniforme).

Déjà nous sommes d'accord que rand file une loi uniforme.
et ce que j'essaie de te faire dire, c'est qu'on peut simuler une distrib uniforme dans un quadrillage avec deux lois uniformes, une pour les lignes, une pour les colonnes.

Considère les colonnes où la sortie des X est dans les classes à 25%.
Considère les cases des X sélectionnés et dont le Y est dans les classes 25%.
Maintenant, fais la même chose avec les classes 2%.
Le tirage est suivant une loi uniforme, mais crois-tu que les cases dans l'un et l'autre cas auront le même nombre de villes, ou un nombre presque équivalent ?

un nombre presque équivalent.

[Dlzlogic]

C'est justement pas ce que dit le théorème centrai limite
Tirage aléatoire == loi uniforme --> répartition suivant la loi normale.
J'ai l'impression que toute la difficulté vient de l'attribution "loi" à une distribution aléatoire, d'une part, comparée à l'attribution "loi" à la loi normale.
En tout cas, il me parait évident qu'une étude systématique, type quadrillage, donnera une répartition uniforme, alors qu'un tirage avec rand ne donnera pas une répartition uniforme. On peut se poser la question "quel écart accepte-t-on". En tout cas, c'est l'origine de ce fil.
On peut, à l'intérieur de chaque case, moduler X et Y suivant une répartition aléatoire.
[HS] Ca me rappelle les dessins avec un graphisme aléatoire (végétation) que j'ai fait vers les années 80. A cette époque, la fonction rand n'existait pas, il fallait se débrouiller autrement [/HS]

[fatal_error]

Tirage aléatoire == loi uniforme

non

tu prends deux boules rouges et une boule verte que tu mets dans une urne. Tu fais un tirage (aléatoire) d'une boule et tu regardes sa couleur.

est-on d'accord que la proba de tirer une boule rouge est plus grande que celle de tirer une boule verte?

[Arkhnor]

Bonjour.

les variables sont de variables aléatoires, donc équiprobable, c'est ce qu'on appelle une loi uniforme.

des évènement aléatoires, donc qui suivent une loi uniforme

les évènements doivent satisfaire aux conditions du hasard, c'est à dire une loi uniforme.

Tirage aléatoire == loi uniforme

C'est totalement aberrant de voir que la notion de hasard est assimilée à la loi uniforme. Va donc lire la définition de variable aléatoire, et dis moi où tu vois la loi uniforme dans cette définition.

Ce problème t'a déjà été signalé plusieurs fois, mais tu n'en as jamais tenu compte. Il est véritablement insupportable de discuter avec quelqu'un qui fait semblant de ne pas voir les arguments des autres lorsqu'ils tombent juste.
J'en ai déjà fait les frais avec toi, alors je n'interviendrai pas plus sur ce sujet.