Bonjours a tous ! Voici une limite en (0,0) d'une fonction a deux variable je vous met au défit de la résoudre ;)
f(x,y)= (|x|^a *y)/(x^2+y^4) a discuter suivant les valeur de a
bon courage :bad2: :happy2:
Limite d'une fonction a deux variables TRES TRES DURE
9 messages
- Page 1 sur 1
Bon on va donner les détails pour montrer que ce n'est pas non plus diabolique comme l'indique l'émoticon du premier message.
Si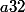 alors on a que
alors on a que \| =\|x\|^{a-3/2}\cdot\fr{\|x\|^{3/2}\|y\|}{x^2+y^4}) et il reste à montrer que la quantité à droite est bornée au voisinage de
et il reste à montrer que la quantité à droite est bornée au voisinage de ) . On peut pour cela utiliser le changement
. On peut pour cela utiliser le changement 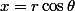 et
et 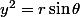 (on ne se contente que des
(on ne se contente que des  positifs, mais la fonction est impaire en la seconde varirable) pour avoir que
positifs, mais la fonction est impaire en la seconde varirable) pour avoir que 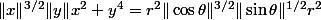 ce qui est bien borné.
ce qui est bien borné.
Conclusion : la limite n'existe que si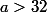 et vaut dans ce cas
et vaut dans ce cas  .
.
Mais je m'aperçois qu'en fait ça n'a rien d'un vrai défi, mais que ça ressemble plutôt à un exercice "classique" sur les fonctions de plusieurs variables".
Si
Conclusion : la limite n'existe que si
Mais je m'aperçois qu'en fait ça n'a rien d'un vrai défi, mais que ça ressemble plutôt à un exercice "classique" sur les fonctions de plusieurs variables".
C'est un peu pour ça que je tenais pas particulièrement à donner la réponse... :hum:girdav a écrit:Mais je m'aperçois qu'en fait ça n'a rien d'un vrai défi, mais que ça ressemble plutôt à un exercice "classique" sur les fonctions de plusieurs variables".
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
C'est un peu pour ça que je tenais pas particulièrement à donner la réponse... :hum:girdav a écrit:Mais je m'aperçois qu'en fait ça n'a rien d'un vrai défi, mais que ça ressemble plutôt à un exercice "classique" sur les fonctions de plusieurs variables".
Sinon, voila ma méthode :
Si
Si
Si
Donc, dans tout les cas,
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
J'ai hésité aussi à donner les détails pour ce défi fictif. Je pense que ceci est un moyen de contourner le fait que l'on ne puisse pas donner les réponses. Mais l'auteur nous a lancé un "défit" et il fallait aussi faire apparaître le fait que ça n'en était pas vraiment un.
Mais si l'auteur en a d'autres...
Mais si l'auteur en a d'autres...
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
