Limite d'une fonction a deux variables
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Meepo
- Messages: 8
- Enregistré le: 02 Mai 2016, 13:22
-
 par Meepo » 13 Sep 2016, 22:14
par Meepo » 13 Sep 2016, 22:14
Bonjour a tous,
Je dois trouver la limite
 \rightarrow (0,0))
de la fonction

en utilisant le theoreme du sandwich.
J'ai approche la fonction selon les courbes
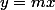
,
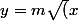,)
et il semble que la limite est 0 (je sais que la limite est 0), mais je n'arrive pas a trouver une bonne inegalite pour le prouver!

Je dois ensuite prouver le cas plus general, cad
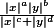
a une limite de 0 pour
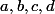
positifs, si
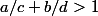
.
Ca fait longtemps que je bloque, svp aidez moi. Merci


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Sep 2016, 22:40
par Ben314 » 13 Sep 2016, 22:40
Salut.
Je sais pas ce que c'est le "théorème du sandwich" et il y a des tas de façon de majorer la fonction pour le montrer.
Une parmi d'autres :
- Si
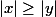
alors
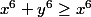
et
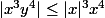
donc
|\leq\frac{|x|^7}{x^6}=|x|)
- Si
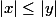
alors
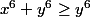
et
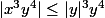
donc
|\leq\frac{|y|^7}{y^6}=|y|)
BILAN : pour tout (x,y) autre que (0,0), on a
|\leq \text{ Max}(|x|,|y|))
ce qui permet de conclure.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Meepo
- Messages: 8
- Enregistré le: 02 Mai 2016, 13:22
-
 par Meepo » 13 Sep 2016, 22:43
par Meepo » 13 Sep 2016, 22:43
Bon, je n'avais pas penser a considérer des cas x <= y et y <= x, merci.
Comment vous faîtes pour voir la solution de tant d'exos aussi facilement??

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Sep 2016, 22:49
par Ben314 » 13 Sep 2016, 22:49
C'est comme dans tout les autres domaines, c'est à force de pratiquer qu'on progresse.
Une méthode qui semble "magique" la première fois qu'on la voie (ou que justement on ne la voie pas...) devient "normale" quand c'est la 3em fois qu'on l'utilise puis "banale" lorsque c'est la 50em fois...
P.S. J'enseigne les maths depuis environ 30 ans donc la pratique je commence à en avoir un peu...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités