Limite de fonction a deux variables

[road runner]

bonsoir
je dois calculer certaine limite et j'ai eu ces resultats

n'existe pas.

n'existe pas aussi

pour j'ai trouver -1 quand j'ai remplacé par f(1/n,1/n) mais je narrive pas a majorer ,,,,

et que ce que je fais pour avec a appartenant a R.

et pour avec a appartenant a R.

merci d'avance

[mathelot]

pour j'ai trouver -1 quand j'ai remplacé par f(1/n,1/n) mais je narrive pas a majorer ,,,,

l'astuce c'est de passer en coordonnéées polaires dès que l'on étudie
une fraction rationnelle homogène en x et y.

et que ce que je fais pour avec a appartenant a R.

a pour limite à cause du thm de la moyenne.

[road runner]

ok j'vais voir

et pour les autres ??

[mathelot]

et pour avec a appartenant a R.

ce qui suggère le changement de variable


intuitivement a pour limite le nombre dérivée de
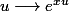
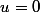
en et , ie, .

euh :hum: , pour faire la démo de ce dernier résultat, on écrit:

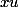
et le produit a pour limite zéro quand

[road runner]

a pour limite à cause du thm de la moyenne.

comment on utilise ici, le thm de la moyenne

[fahr451]

bonsoir

pour j'ai trouver -1 quand j'ai remplacé par f(1/n,1/n) mais je narrive pas a majorer ,,,,


merci d'avance

bonsoir
es- tu sûr ?

la limite n'existe pas

[road runner]

pardon
en fait c'est ici que mathelot a utilisé la moyenne

[fahr451]

il existe c compris entre x et y (ou l'inverse) tel que l'intégrale vaille cos(c)
c coincé entre xet y tend vers a d'où la limite égale à cos a

[road runner]

ok *merci

[mathelot]

Ensuite, pour montrer l'absence de limite, on considère deux limites
radiales différentes, selon deux droites passant par l'origine , d'équation =constante. Içi, ce n'est pas la peine, car la fonction en valeur absolue, tend vers sauf pour quelques valeurs de particulières.

[fahr451]

f(x,0) devrait suffire pour conclure