Isomorphisme

par **LA solution** » 03 Oct 2013, 18:11

bonjour,
jaimerai avoir une idee de la construction de l isomorphisme qui part d un groupe a un autre et comment montrer que ces deux groupes sont isomorphes c est a dire qu il existe une bijection de l un sur l autre par exemple
soit f une application:

par **LA solution** » 03 Oct 2013, 18:22

en realite ça ma paru difficil car je n ai pa la fonction f comme d abititude entre les mains sinon il suiffisai de verifier 1)que f est homomorphisme2)et de montrer ensuite qu elle est bijective

par **eratos** » 03 Oct 2013, 20:18

LA solution a écrit:en realite ça ma paru difficil car je n ai pa la fonction f comme d abititude entre les mains sinon il suiffisai de verifier 1)que f est homomorphisme2)et de montrer ensuite qu elle est bijective

tu peux penser au logarithme je crois :lol3:
Pour le reste... (je viens juste de commencer l'étude des groupes)

par **capitaine nuggets** » 04 Oct 2013, 08:28

Salut !

eroatos a raison : le logarithme est un isomorphisme du groupe

vers le groupe

.

En effet, quels que soient

donc

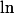
est un morphisme.
De plus,

est bijective.
Par conséquent,

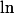
est un isomorphisme.

par **LA solution** » 04 Oct 2013, 13:36

Merci mon capitaine et a vos ordres
j ai tres bien compris

par **Archibald** » 04 Oct 2013, 13:53

capitaine nuggets a écrit:Salut !

eroatos a raison : le logarithme est un isomorphisme du groupe vers le groupe .

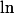
En effet, quels que soient donc est un morphisme.
De plus, est bijective.
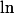
Par conséquent, est un isomorphisme.

C'est plutôt :

par **deltab** » 04 Oct 2013, 14:26

Bonjour.

Archibald a écrit:C'est plutôt :

et l'isomorphisme réciproque est la fonction exponentielle

,

. On a bien

.

Isomorphisme

isomorphisme

Qui est en ligne