Isomorphisme d'anneaux

[congov]

Bonjour,

je suis devant un exercices de mon cours d'algèbre et mon j'ai beaucoup de mal à appliquer ma théorie à ce problème:

Soit R1 =Fp[X]/(X^2;)1), R2 =Fp[X]/(X^2+4). Déterminer si R1 et R2 sont isomorphe
pour p = 2,5,7

Quelqu'un pourrait-il me mettre sur la voie?

Merci d'avance

[Ben314]

Salut,
Quelques éléments d'approche... :
Le polynôme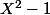 n'est jamais irréductible (sur aucun des corps Fp) donc Fp[X]/(X^2-1) est systématiquement un anneau non intégre (et les diviseurs de zéro sont...)
Par contre, le polynôme X^2+4 est... des fois... irréductible sur Fp et dans ce cas Fp[X]/(X^2+4) est un corps et ne risque pas d'être isomorphe à un truc non intègre. Si ce n'est pas le cas, qui sont les diviseurs de zéro de cet anneau ?
Si on les envoie sur les diviseurs de zéro de Fp[X]/(X^2-1), est-ce que cela nous fait un morphisme d'anneau ?