Intro à la topologie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
SamAz
- Membre Naturel
- Messages: 55
- Enregistré le: 29 Jan 2021, 12:54
-
par SamAz » 23 Mar 2021, 17:18
Bonsoir,
J'aimerai bien une petite aide, si possible, pour un exercice typique sur les normes. J'ai a montrer qu'une certaine application est une norme sur R2, je bloque sur la demonstration de l'inegalité triangulaire. Je sais qu'il faut utiliser l'inegalité de Cauchy-Schwarz mais j'arrive pas a savoir comment. Mon application est:
Pour tout
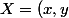\in \mathbb{R}<br />^{2}, N(X)=|x|+\sqrt{x^2+y^2})
-
mathelot
par mathelot » 23 Mar 2021, 18:31
il suffit de démontrer que
réels
si
)
et
)
alors
 \leq N(X)+N(Y))
il suffit de montrer que
^2+(y_1+y_2)^2} \leq \sqrt{x_1^2+y_1^2}+\sqrt{x_2^2+y_2^2})
ce qui se fait en élevant deux fois au carré les inégalités et en simplifiant à chaque élévation au carré
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
