Proba coef binomiaux (niveau intro)

[zuko]

Bonjour a tous et bonne année!

question : je suis cette video en intro aux probas [en ANGLAIS!]
https://www.youtube.com/watch?v=KbB0FjPg0mw&t=82s
à 37:40
le prof demontre comment écrire k parmi n (il veut en arriver à (n k) = n!/ (n-k)! . k!)
au debut il denombre : n(n-1)(n-2)...(n-k+1)
et ensuite il divise par k! (k factorielle).
Pouquoi?

merci!

[ijkl]

le prof demontre comment écrire k parmi n

Bonjour

c'est illisible

désolé mais relisez -vous

Vous ne pourriez pas essayer de faire des recherches par vous même (franchement enfermez vous dans votre chambre (c'est la bonne période avec le confinement) et faites des calculs

c'est bien d'avoir un prof (tout le monde n'a pas eu cette chance)

Si votre prof vous donne des formules c'est parce que vous avez cherché un peu et qu'il vous a guidé pour les trouver

c'est pas une critique c'est juste qu'en combinatoire je ne crois pas au mec qui nous balance une formule sans l'avoir comprise donc sans l'avoir cherché mais là j'ai pas l'impression que vous avez cherché un truc vous nous balancez une formule et demandez pourquoi elle est comme ça

[GaBuZoMeu]

Bonsoir,

Je suppose que la méthode est la suivante :
choisir un 1er élément (n possibilités), un 2e (n-1 possibilités),...,un k-ème (n-k+1 possibilités).
On a k éléments parmi n, rangés en une liste ordonnée. Combien y a-t-il de façons d'ordonner k éléments ?

@ijkl : tu viens de te faire sanctionner sur ilemaths pour ton comportement. Ne crois-tu pas qu'il serait bon de mettre la pédale douce ?

[zuko]

Bonjour @ijkl,
Tu imagines des scénarios et tu es hors sujet.

Je n'ai pas de prof.
J'ai 35 ans, ai fait des études de droit puis travaillé dans la transparence en finance.
J'ai demandé de l'aide. Je n'ai pas exigé de l'aide.
Il s'agit d'une vidéo libre sur youtube. Plus je cherche d'autres sources/ poly et moins je trouve.

Je ne crois pas que tu puisses m'aider mais même si tu pouvais : Ôte-toi de mon soleil!!!

[ijkl]

@ijkl : tu viens de te faire sanctionner sur ilemaths pour ton comportement. Ne crois-tu pas qu'il serait bon de mettre la pédale douce ?

Vous m'avez reconnnu GBZM (heu oui améthyste c'est moi)

ok je vais aller dormir : je suis sage (enfin j'essaye de l'être)

Merci pour votre patience avec moi

signé un type qui vous admire (eh oui on a le droit d'admirer les gens )

[mathelot]

on compte les k-listes de longueur k sans répétition d'éléments d'un ensemble de cardinal n. on compte l'ordre .
par exemple , la 3-liste (3,2,1) n'est pas égale à la 3-liste (2,3,1)

des k-listes d'éléments d'un ensemble E de n éléments , il y en a n(n-1)(n-2)....(n-(k-1))

il y a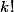 k-listes qui ont les mêmes éléments.

par exemple (3,2,1),(2,3,1) (3,1,2) (2,1,3) (1,2,3) (1,3,2) soit 3!=6 listes qui ont les mêmes éléments.

En divisant par k!, le nombre total de k-listes, on compte le nombre de combinaisons (parties à k éléments d'un ensemble à n éléments) sans ordre sur les éléments
(par exemple, la partie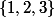 correspond aux 6 "3-listes" de longueur 3.

plus généralement, le nombre de combinaisons de k éléments tirés d'un ensemble à n éléments est

(*)

En suite on multiplie haut et bas par (n-k)!
on trouve
(**)

l'égalité (*) sert pour le calcul de
l'égalité (**) sert pour les applications théoriques

[ijkl]

Je présente mes excuses à Zuko

Merci à GBZM et Zuko pour votre compréhension

je ne suis pas parfait ok mais j'essaye de devenir moins con

[zuko]

Je présente mes excuses à Zuko

Merci à GBZM et Zuko pour votre compréhension

je ne suis pas parfait ok mais j'essaye de devenir moins con

-> acceptées, j'ai eu ton âge moi aussi

[ijkl]

[-> acceptées, j'ai eu ton âge moi aussi

merci

et encore mes excuses

en fait j'ai 55ans mais bon j'ai souvent l'impression d'avoir dix ans(sérieux il n'y a aucune ironie dans cette remarque)

bonne année à vous

[zuko]

merci @GaBuZoMeu, @Mathelot :
c'est cette partie que je n'avais pas comprise:

il y a k-listes qui ont les mêmes éléments.

En divisant par k!, le nombre total de k-listes, on compte le nombre de combinaisons (parties à k éléments d'un ensemble à n éléments) sans ordre sur les éléments

@ijkl, pas de soucis je vais essayer d'apprendre comment coder les formules, factorielles pour les prochaines fois
Bonne soirée à tous