Je fais un exercice qui me pose quelques soucis, et j'aimerais quelques unes de vos explications !
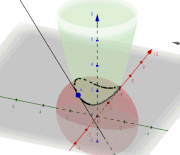
Je dois déterminer la représentation paramétrique de la droite tangente à la courbe d'intersection entre
Par mon cours, je sais qu'une surface (qu'on ne peut pas représenter par une fonction) de
- une équation (style sphère, cylindre, etc.)
- des surfaces de niveau d'une fonction de
Encore par mon cours, l'équation du plan tangent à la surface en un point
Je me demande alors :
Si l'on définit la courbe d'intersection comme une "courbe de niveau" d'une fonction de deux variables, et qu'on exploite le même raisonnement que précédemment: est-ce que la droite tangente au point en question est tout simplement le produit scalaire du gradient de la fonction de deux variables par le vecteur position ? Le problème que j'ai avec cette démarche est que l'on obtient une droite du plan, qui ne dépend pas de z, ce qui n'a pas vraiment de sens.
Merci d'avance aux personnes qui m'expliqueront mes erreurs et la démarche effective.