Interpolation par séries entières
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Landstockman
- Membre Relatif
- Messages: 188
- Enregistré le: 11 Aoû 2015, 07:22
-
 par Landstockman » 20 Déc 2017, 15:50
par Landstockman » 20 Déc 2017, 15:50
Bonjour à tous,
Depuis quelques temps je me pose la question suivante :
Soit
_{n\in\mathbb N})
une suite de complexes qui vérifie :
\in \mathbb N^2, i\neq j \Longrightarrow |x_i-x_j|>d)
Soit
_{n \in \mathbb N}\in \mathbb C^{\mathbb N})
.
Existe-t-il f une fonction développable en série entière en 0 (elle sera donc de rayon infini) telle que
=y_i)
?
Sinon, pouvons-nous trouver une condition nécessaire et suffisante à l'existence d'une telle fonction ?
Merci d'avance
-
aviateur
 par aviateur » 29 Nov 2018, 20:54
par aviateur » 29 Nov 2018, 20:54
Bjr
Je ne sais pas ce que tu veux résoudre en posant cette question. Mais sans conditions drastiques sur les

et

il n' y a pas de solutions (penser au principe du maximum).
-
Landstockman
- Membre Relatif
- Messages: 188
- Enregistré le: 11 Aoû 2015, 07:22
-
 par Landstockman » 29 Nov 2018, 21:05
par Landstockman » 29 Nov 2018, 21:05
Justement, si tu regardes bien, les conditions que j'ai imposées mettent en défaut les hypothèses du principe du maximum.
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 29 Nov 2018, 21:51
par LB2 » 29 Nov 2018, 21:51
Bonjour,
C'est une sorte de réciproque du principe des zéros isolés?
-
Landstockman
- Membre Relatif
- Messages: 188
- Enregistré le: 11 Aoû 2015, 07:22
-
 par Landstockman » 29 Nov 2018, 21:54
par Landstockman » 29 Nov 2018, 21:54
Ça serait un peu l'idée LB2 !
Après je ne sais pas du tout si c'est vrai
-
aviateur
 par aviateur » 30 Nov 2018, 14:16
par aviateur » 30 Nov 2018, 14:16
Bjr
Le principe des zéros isolés, je ne pense pas car les

ne sont pas nuls.
Franchement poser une question générale (et vague à mon sens) ne donnera pas de réponses. Il faut être plus modeste, i.e .
Commencer par donner une suite (x_i) et (y_i) et voir déjà si on est capable de répondre.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 30 Nov 2018, 14:28
par Ben314 » 30 Nov 2018, 14:28
Salut,
Landstockman a écrit:Soit
_{n\in\mathbb N})
une suite de complexes qui vérifie :
\in \mathbb N^2, i\neq j \Longrightarrow |x_i-x_j|>d)
Soit
_{n \in \mathbb N}\in \mathbb C^{\mathbb N})
.
Existe-t-il f une fonction développable en série entière en 0 (elle sera donc de rayon infini) telle que
=y_i)
?
La réponse est oui (et il y a même une infinité de solutions)
C'est un résultat très classique de la théorie qu'on obtient en utilisant les "facteurs primaires" de Weierstrass.
Tu trouvera des preuve (pas très compliquée) dans tout les bouquins classiques sur le sujet (ainsi que sur le net) sans doute dans le chapitre dédié au "Théorème de factorisation de Weierstrass".
On peut même faire un peu mieux en montrant qu'il existe une fonction méromorphe sur U (domaine donné de C pouvant être égal C tout entier comme dans ton cas) ayant des pôles données d'avance sur un ensemble discret D fixé d'avance de U : c'est le théorème dit "de Mittag-Leffler".
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
aviateur
 par aviateur » 30 Nov 2018, 14:49
par aviateur » 30 Nov 2018, 14:49
Bjr
Si on prend
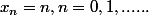
et
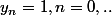
Pour tout
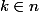
on pose
= cos(2 k \pi z))
Les fonctions

sont analytiques et sont solutions. on ne trouve pas une fonction développable en séries entières avec rayon infini et je ne vois pas comment on va caractériser toutes les fonctions entières qui répondent à la question.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 30 Nov 2018, 16:21
par Ben314 » 30 Nov 2018, 16:21
Je comprend pas trop ce que tu dit : tes fonction

sont on ne peut plus clairement "entières" c'est à dire analytique sur C tout entier, c'est à dire développable en série entière au voisinage de 0 (ou de tout autre point) avec un rayon de C.V. infini.
Et elles sont toutes solutions du problème "f(n)=1 pour tout n dans N" ce qui signifie bien que le problème admet (comme toujours) une infinité de solutions.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
aviateur
 par aviateur » 30 Nov 2018, 16:53
par aviateur » 30 Nov 2018, 16:53
Oui tout à fait. Mais perso j'ai compris la question (vu le titre "interpolation par série entière") la recherche d'une fonction entière qui approxime "quelque chose" (une fonction? ) qui prend les valeurs y_i en les x_i. Un peu comme une généralisation de l'interpolation polynomiale d'une fonction vérifiant f(x_i)=y_i,i=0,1,....,n que l'on cherche dans un espace de polynômes de degré n.
La donnée des (x_i,y_i) dans le cas de la question ne définit aucunément la série entière
et toute série entière qui vérifie f(x_i)=y_i "solution" ne vérifie que cette condition et rien d'autre.
Derrière chaque question il y a un objectif. Ici je me demande si le titre sous entend qu'il y a un but du genre "approximation". Du moins c'est que j'ai cru comprendre.
-
Landstockman
- Membre Relatif
- Messages: 188
- Enregistré le: 11 Aoû 2015, 07:22
-
 par Landstockman » 30 Nov 2018, 21:01
par Landstockman » 30 Nov 2018, 21:01
Merci Ben !
Aviateur je ne comprends pas bien ce que tu veux dire, l'idée c'était bien d'interpoler, mais je ne vois pas très bien où est le problème...
-
aviateur
 par aviateur » 01 Déc 2018, 11:31
par aviateur » 01 Déc 2018, 11:31
Bonjour
Qu'entends tu par interpoler? C'est uniquement trouver une fonction entière qui vérifie
=y_i, i\in \N?)
Personnellement, j'imagine toujours que derrière ce genre de question, il y a un objectif. Maintenant si il n'y en a pas, effectivement tu ne peux pas me comprendre.
-
Landstockman
- Membre Relatif
- Messages: 188
- Enregistré le: 11 Aoû 2015, 07:22
-
 par Landstockman » 01 Déc 2018, 12:21
par Landstockman » 01 Déc 2018, 12:21
C'est bien ça
Non il n'y avait pas d'objectif particulier, ceci explique cela
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
