Injection de Q dans N
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Victhemath
- Membre Naturel
- Messages: 80
- Enregistré le: 26 Oct 2013, 16:56
-
 par Victhemath » 06 Déc 2013, 15:14
par Victhemath » 06 Déc 2013, 15:14
Bonjour, je dois exhiber une injection de

dans

. J'ai un exemple du cours où l'on me donne la fonction :
+1}3^{|p|}5^{q})
avec
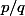
sous la forme irréductible.
Quelqu'un peut m'expliquer ?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 06 Déc 2013, 15:43
par arnaud32 » 06 Déc 2013, 15:43
-
Victhemath
- Membre Naturel
- Messages: 80
- Enregistré le: 26 Oct 2013, 16:56
-
 par Victhemath » 06 Déc 2013, 15:46
par Victhemath » 06 Déc 2013, 15:46
Merci pour la réponse ! J'en ai désormais une autre :)
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 06 Déc 2013, 15:49
par arnaud32 » 06 Déc 2013, 15:49
Victhemath a écrit:Bonjour, je dois exhiber une injection de

dans

. J'ai un exemple du cours où l'on me donne la fonction :
+1}3^{|p|}5^{q})
avec
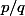
sous la forme irréductible.
Quelqu'un peut m'expliquer ?
tu verifie que ta fonction est bien a valeur dans N (ce qui est vrai car 1+sign(p) ; |p| et q sont positifs
ensuite tu verifie l'injectivite en regardant f(p/q)=f(r/s)
tu utilises le fait que 2, 3 et 5 sont premiers
-
Victhemath
- Membre Naturel
- Messages: 80
- Enregistré le: 26 Oct 2013, 16:56
-
 par Victhemath » 07 Déc 2013, 17:13
par Victhemath » 07 Déc 2013, 17:13
Bonsoir. Pour montrer l'injectivité, je me retrouve avec ça :
+1}3^{|p|}5^{q})
=
+1}3^{|p'|}5^{q'})
Comment j'en viens à montrer que p/q=p'/q' ?
-
Victhemath
- Membre Naturel
- Messages: 80
- Enregistré le: 26 Oct 2013, 16:56
-
 par Victhemath » 07 Déc 2013, 17:24
par Victhemath » 07 Déc 2013, 17:24
Je ne sais pas si on a le droit au double post ici mais je pose ma question :
Il y a dans mon cours, Q (ensemble des rationnels) n'est pas complet, il existe des parties bornées de Q sans sup. Quelqu'un peut-il me donner un exemple ?
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 07 Déc 2013, 18:57
par jlb » 07 Déc 2013, 18:57
{x rationnels/ x²=<2} doit convenir

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Déc 2013, 18:57
par Ben314 » 07 Déc 2013, 18:57
Oui,
Par exemple l'ensemble des rationnels positifs dont le carré est inférieur à 2.
Dans R la borne supérieur serait sqrt(2) et dans Q... y'en a pas..
Edit : grillé...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Victhemath
- Membre Naturel
- Messages: 80
- Enregistré le: 26 Oct 2013, 16:56
-
 par Victhemath » 07 Déc 2013, 19:35
par Victhemath » 07 Déc 2013, 19:35
Merci pour l'exemple ! Et sinon pour mon injection, une idée ? :)
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 07 Déc 2013, 19:40
par jlb » 07 Déc 2013, 19:40
Victhemath a écrit:Merci pour l'exemple ! Et sinon pour mon injection, une idée ?

relis le message d'Arnaud32!!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Déc 2013, 20:26
par Ben314 » 07 Déc 2013, 20:26
Victhemath a écrit:Merci pour l'exemple ! Et sinon pour mon injection, une idée ?

Tu utilise
l'unicité de la décomposition d'un entier en facteurs premiers qui te dit que, si

alors on a obligatoirement

,

,

, ...
C'est en fait là toute "l'astuce" de la formule : avec une unique égalité entre deux trucs, tu en déduit une multitude d'égalités...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Victhemath
- Membre Naturel
- Messages: 80
- Enregistré le: 26 Oct 2013, 16:56
-
 par Victhemath » 08 Déc 2013, 18:31
par Victhemath » 08 Déc 2013, 18:31
Ha oui, j'aurais du le voir ! Merci !
J'ai une autre question, il y a dans mon cour que une intersection infinie d'ouverts n'est pas un ouvert.
On me donne l'exemple de ]-1/n,1/n[ avec n E N\{0}
Quelqu'un pour me détailler l'idée ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 08 Déc 2013, 18:34
par Ben314 » 08 Déc 2013, 18:34
Un réel x, il est dans l'intersection de tout tes ouverts, ssi il vérifie -1/n<x<1/n pour tout entier n.
Si tu fait tendre n vers l'infini, ça te dit que...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Victhemath
- Membre Naturel
- Messages: 80
- Enregistré le: 26 Oct 2013, 16:56
-
 par Victhemath » 08 Déc 2013, 18:46
par Victhemath » 08 Déc 2013, 18:46
Par ce que x devient le singleton 0 et que ce n'est pas un intervalle ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 08 Déc 2013, 19:05
par Ben314 » 08 Déc 2013, 19:05
Victhemath a écrit:Par ce que x devient le singleton 0 et que ce n'est pas un intervalle ?
Si on veut parler "carré carré", x est effectivement forcément nul donc l'intersection de tout tes ouverts est le singleton {0}.
Après, vu les définitions usuelles, il me semble qu'un singleton c'est bien un intervalle ({a}=[a,a]), mais pas un intervalle ouvert...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Victhemath
- Membre Naturel
- Messages: 80
- Enregistré le: 26 Oct 2013, 16:56
-
 par Victhemath » 08 Déc 2013, 19:28
par Victhemath » 08 Déc 2013, 19:28
ok ! Merci Ben :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
 dans
dans  . J'ai un exemple du cours où l'on me donne la fonction :
. J'ai un exemple du cours où l'on me donne la fonction :+1}3^{|p|}5^{q}) avec
avec 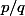 sous la forme irréductible.
sous la forme irréductible.dans
. J'ai un exemple du cours où l'on me donne la fonction :
avec
sous la forme irréductible.
