Image espace vectoriels

[Dante0]

Donc quand on cherche l'image de g c'est l'ensemble des colonnes telles que C1 = Bc1,C2=Bc2,C3=Bc3 ?

[Anonyme]

Je vois toujours pas ou tu veux en venir...
Ah... Tu as fait le produit de B et de la 3e colonne...

C'est quoi la 3ième colonne ?

Désolé : Ceci est mon dernier message car je donne de nouveau le conseil de relire ton cours...

[Dante0]

C'est quoi la 3ième colonne ?

Désolé : Ceci est mon dernier message car je donne de nouveau le conseil de relire ton cours...

Tu l'a sorti d'ou le vecteur de ton exemple ? Je pensais que c'etait en lien avec l'exercice, c'etait juste une coincidence en fait.
Du coup j'ai toujours pas compris. Et je sais tout ce qu'il faut savoir pour mon cours (qui n'est pas très poussé évidemment).

[Anonyme]

C'est parce que c'est la nouvelle année et qu'on doit être TOUS sympas les uns avec les autres
(c'est ce que j'ai promis au père Noel pour qu'il m'apporte des cadeaux)

que je t'écris un autre message pour t'aider à comprendre :

L'application linéaire g est une application de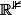 dans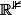

et le vecteur (0,0,1) est un des vecteurs de la base dite "canonique" de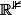

ps)
Comme l'E.V.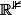 est de dimension 3 , il existe une base constituée de 3 vecteurs....

[Dante0]

C'est parce que c'est la nouvelle année et qu'on doit être TOUS sympas les uns avec les autres
(c'est ce que j'ai promis au père Noel pour qu'il m'apporte des cadeaux)

que je t'écris un autre message pour t'aider à comprendre :

L'application linéaire g est une application de dans

et le vecteur (0,0,1) est un des vecteurs de la base dite "canonique" de

ps)
Comme l'E.V. est de dimension 3 , il existe une base constituée de 3 vecteurs....

J'ai pas cette propriété dans mon cours... :triste:
Tu peux la terminer je suis sur que je vais comprendre! A force de parler en sous-entendu je ne fais que m'enfoncer dans mon ignorance :mur:

[Anonyme]

J'ai pas cette propriété dans mon cours... :triste:

Ne sois pas triste et encore une fois relis ton cours... et essaie de le lire et de le re-lire jusqu'à que tu le comprennes...

Piste de travail : Comme la matrice de ton exo est une matrice (3,3) ,
l'application linéaire associée à cette matrice est une application de dans un espace vectoriel qui de dimension inférieure ou égale à 3

ps)
Comme tu as écrit que

Pour info le corrigé dit que img = x(-2,0,2) +y(1,0,2) +z(1,-1,-1) avec x,y,z réels en colonne bien sur.

, l'application linéaire associée à la matrice est une application de dans

Pour trouver une base de , il suffit de trouver l'image de la base canonique de et de montrer que ces 3 vecteurs images sont "libres"


Tous mes voeux pour cette nouvelle année

[Dante0]

Ne sois pas triste et encore une fois relis ton cours... et essaie de le lire et de le re-lire jusqu'à que tu le comprennes...

Piste de travail : Comme la matrice de ton exo est une matrice (3,3) ,
l'application linéaire associée à cette matrice est une application de dans un espace vectoriel qui de dimension inférieure ou égale à 3

ps)
Comme tu as écrit que , l'application linéaire associée à la matrice est une application de dans

Pour trouver une base de , il suffit de trouver l'image de la base canonique de et de montrer que ces 3 vecteurs images sont "libres"


Tous mes voeux pour cette nouvelle année

On cherche img ou la base de img la ?

En faisant ce que tu dis (multiplier B par le colonnes de la base canonique de R3) je retombe sur la matrice B...

[Anonyme]

J'ai essayé de t'expliquer au mieux que je pouvais...Désolé...

ps)
dernier conseil :
Essaie de relire tous les messages dans cette discussion ou de relire ton cours

A+

[Nightmare]

Arriverais-tu dans un premier temps à calculer les images par g des vecteurs de la base canonique?

[Dante0]

Arriverais-tu dans un premier temps à calculer les images par g des vecteurs de la base canonique?

Je pense, je suis pas sur.
Vous parlez beaucoup en sous-entendu, j'arrive pas à comprendre ce que vous dites..
g(X) = BX on est d'accord ? Si X est le premier vecteur de la base canonique de R3 il suffit de multiplier B par ce vecteur non ? Idem pour les 2 autres. On finit par tomber sur la matrice B...

[Nightmare]

Qu'est-ce que tu considères comme sous-entendu dans ma question précédente? Elle était pourtant explicite.

Oui, g(X)=BX, donc que valent les images des vecteurs de la base canonique? Saurais-tu en déduire l'image d'un vecteur (x,y,z) quelconque ?

[Dante0]

Qu'est-ce que tu considères comme sous-entendu dans ma question précédente? Elle était pourtant explicite.

Oui, g(X)=BX, donc que valent les images des vecteurs de la base canonique? Saurais-tu en déduire l'image d'un vecteur (x,y,z) quelconque ?

Je viens de répondre à cette question non ? :hein:
Avec un vecteur quelconque il suffit de faire le produit de B et de la matrice colonne (x,y,z) et ca donne la réponse que j'ai donné plus haut à savoir img = x(-2,0,2) +y(1,0,2) +z(1,-1,-1)

[Nightmare]

A quel moment es-tu censé avoir répondu à la question?

Je ne vois nulle part écrit g(e1)=... , g(e2)=...., g(e3)=....

Concernant la suite, im(g) est un espace vectoriel, comment un espace vectoriel peut-il être égal à "x(-2,0,2) +y(1,0,2) +z(1,-1,-1)" qui lui est un vecteur? Attention à ce que tu écris.

Im(g) est l'espace vectoriel des images par g. A rigueur près, tu sais maintenant plus ou moins comment s'écrit un vecteur de Im(g) : Il est de la forme x(-2,0,2) +y(1,0,2) +z(1,-1,-1). Peux-tu en déduire une base de cet espace vectoriel?

[Dante0]

A quel moment es-tu censé avoir répondu à la question?

Je ne vois nulle part écrit g(e1)=... , g(e2)=...., g(e3)=....

Concernant la suite, im(g) est un espace vectoriel, comment un espace vectoriel peut-il être égal à "x(-2,0,2) +y(1,0,2) +z(1,-1,-1)" qui lui est un vecteur? Attention à ce que tu écris.

Im(g) est l'espace vectoriel des images par g. A rigueur près, tu sais maintenant plus ou moins comment s'écrit un vecteur de Im(g) : Il est de la forme x(-2,0,2) +y(1,0,2) +z(1,-1,-1). Peux-tu en déduire une base de cet espace vectoriel?

C'est pourtant ce qui est marqué en corrigé.. il faut l'écrire en colonne c'est cela ? SInon il s'écrit comment ? (je précise qu'on parle de l'espace vectoriel img)
La base de imf c'est {(-2,0,2),(1,0,-2)}

[Nightmare]

Ca m'étonnerait que ton corrigé ait écrit, texto, "Im(g)=x(-2,0,2) +y(1,0,2) +z(1,-1,-1)"

Pourquoi la famille de vecteur que tu as cité est-elle bien une base?

[Dante0]

Ca m'étonnerait que ton corrigé ait écrit, texto, "Im(g)=x(-2,0,2) +y(1,0,2) +z(1,-1,-1)"

Pourquoi la famille de vecteur que tu as cité est-elle bien une base?

Parce qu'elle engendre img et que les 2 vecteurs sont libres.
Y'a marqué ca dans le corrigé c'est faux ? Parce que si je me met a apprendre des trucs faux je suis mal barré ^^

[Nightmare]

Parce qu'elle engendre img

Saurais-tu le montrer

et que les 2 vecteurs sont libres.

Attention, ça n'a pas de sens, dire que des vecteurs sont libres ne veut rien dire, par contre une famille de vecteur peut être libre oui.

[Dante0]

Saurais-tu le montrer



Attention, ça n'a pas de sens, dire que des vecteurs sont libres ne veut rien dire, par contre une famille de vecteur peut être libre oui.

Non je ne sais pas le démontrer... :/
C'est parce que c'est l'ensemble des combinaisons linéaires de 2 vecteurs de R3 non ?

[Anonyme]

Attention, ça n'a pas de sens, dire que des vecteurs sont libres ne veut rien dire, par contre une famille de vecteur peut être libre oui.

Là , tu chipotes...

[Nightmare]

Là , tu chipotes...

Non, j'utilise un vocabulaire approprié.

Non je ne sais pas le démontrer... :/
C'est parce que c'est l'ensemble des combinaisons linéaires de 2 vecteurs de R3 non ?

Quelle est la définition d'une famille génératrice? Que faut-il montrer alors?