Idéal principal
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 23 Jan 2008, 12:58
par legeniedesalpages » 23 Jan 2008, 12:58
Bonjour,
Soit
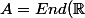)
, comment montrer que tout idéal à gauche est pricinpal et que
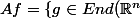,\ ker g \supset ker f \})
.
Merci pour votre aide.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 23 Jan 2008, 13:35
par yos » 23 Jan 2008, 13:35
Salut.
Prends f de rang maximal dans I.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 23 Jan 2008, 21:45
par ThSQ » 23 Jan 2008, 21:45
Joli, sans aucun doute hyper-classique mais joli.
Ca rejoint le résultat sur la factorisation des applications linéaires quand le noyau de l'un est inclus dans l'autre.
Une question logique est de savoir à quoi ressemble les idéaux à droite :bad: (principal aussi) et si tout ça reste vrai en dimension infinie (non : endos de rang fini)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 23 Jan 2008, 23:28
par yos » 23 Jan 2008, 23:28
Et pas commode. S'il s'en sort avec mon indic laconique (ta mère), il est fort.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 24 Jan 2008, 13:14
par ThSQ » 24 Jan 2008, 13:14
Indice moins laconique monique :
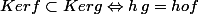
(résultat tout à fait épatant je trouve et valable même en dim infinie, modulo Zorn et son orchestre)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 25 Jan 2008, 09:06
par yos » 25 Jan 2008, 09:06
C'est pas plutôt la partie facile de l'exo?
Ce qui me semble plus dur c'est de montrer que si f est de rang maximal r dans I, alors tout g de I a un noyau contenant Ker f. Je pensais dire que si c'était pas le cas, il y aurait un a de E tel que
=0\neq g(a))
et en combinant f et g, fabriquer un élément de I de rang >r.
Cette dernière combinaison est pas si évidente.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités