Groupe abélien totalement ordonné

[chombier]

Bnjour,
je commenc à me pencher sur le tome 2 d'Arnaudies Fraysse (Analyse) et je suis déjà coincé :


J'imagine qu'il s'agit d'un isomophisme d'ordre, c'est à dire qu'il faut trouver une autre relation d'ordre dans que l'ordre usuel, qui sont compatible avec la loi du groupe, et qui ne soit pas isomorphe à la loi habituelle

Mais alors du coup je n'ai aucune idée, aucune piste. Si quelqu'un voit la lumère... Merci

[aviateur]

Bonjour il s'agit d'un exercice ou d'un passage que tu ne comprends pas? Peux tu donner la page s-t-p?

[chombier]

C'est l'exercice 2 page 6 (édition de 1991), je n'arrive pas à faire le petit b.

[Pseuda]

Bonjour,

(Q+*, x) est déjà un groupe totalement ordonné par l'ordre usuel et la multiplication respecte l'ordre : si a<=b et c<=d, alors ac<=bd. Il pourrait s'agir de trouver un autre ordre, par exemple en jouant sur le dénominateur et le numérateur de la fraction irréductible, par exemple on aurait 3/5 > 7/4 car 5>4 ?

[chombier]

Je pense que c'est ça, il faut trouver un autre ordre. Lui aussi compatible avec la loi du groupe.

Sachant qu'il suffit de savoir comparer un nombre à l'élément neutre 1 :

En posant , il suffit donc de mettre en évidence tel que :



Ainsi


Avec l'ordre usuel,

[aviateur]

Rebonjour
Je ne suis pas sûr. ssi [(p< m) ou (p=m et ] (les fractions sont irréductibles.)

[chombier]

La relation d'ordre que tu proposes n'est pas compatible avec la loi du groupe, car et

or il y a quelque chose de primordial dans un groupe totalement ordonné : si , alors

Le plus dur n'est donc pas de trouver un ordre mais un ordre compatible avec la loi du groupe

D'une façon générale, la relation d'ordre d'un groupe abélien totalement ordonné est déterminée par l'ensemble P de ses éléments positifs . L'ensemble des éléments négatifs est alors

Pour que P définisse un ordre compatible avec la loi du groupe, il faut et il suffit que :




On a alors :

[aviateur]

Oui, j'ai bien compris.
Trouver un ordre compatible n'est pas vraiment difficile mais il ne faut pas l'isomorphisme, c'est vraiment là la difficulté et un exemple semble bien difficile, je suis curieux de voir une solution.

[chombier]

Je reviens sur mon exemple et sur les groupes totalement ordonnés.

Et je propose de définir ainsi :
.

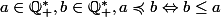
Cette astuce se généralise à tous les groupes ordonnés :

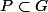
Si est un groupe ordonné, on appelle cône positif de G tout sous-ensemble vérifiant :
(1)
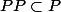
(2)
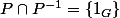
(3)
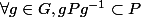
Cette dernière condition étant trivialement vérifiée si G est abélien.

A toute relation d'ordre sur G compatible avec sa loi corresponds un cône positif .

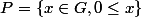
Inversement, à tout cône positif P de G corresponds une relation d'ordre compatible avec la loi
de G : .

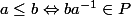
Ainsi,
la condition (1) reviens à dire que est transitive.
la condition (2) reviens à dire que est réflexive et antisymétrique.
la condition (3) reviens à dire que l'ordre est compatible avec la loi du groupe.

Il existe donc une correspondance bijective entre les relations d'ordre compatibles avec G et les cônes positifs de G.

Si l'on souhaite que la relation d'ordre soit totale, il faut ajouter une condition sur P :
(4)

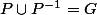
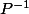
Il y a alors quelque chose d'amusant, c'est que si est un cône positif, alors est un cône positif, qui définit la relation d'ordre duale :


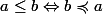
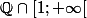
On a ainsi trouvé deux cônes positifs de : et

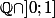
Y en a-t-il d'autres ? Mystère... !

[aviateur]

Bonjour @Chombier Oui mais les deux groupes totalement ordonnés sont isomorphes et c'est que tu ne voulais pas?

[chombier]

Ah oui, le morphisme . Ca s'est vu

Donc le problème reste ouvert. J'aurais quand même avancé sur le sujet en cherchant une solution.

[Skullkid]

Bonjour, j'ai pas fait toutes les vérifs proprement mais à vue de nez ça marche en ordonnant par une valuation p-adique : si ou ( et ). En prenant p = 2 on a

[Mimosa]

Bonjour

L'ordre associé à une valuation p-adique n'est pas total!

[Skullkid]

Pas sûr de comprendre... la valuation est définie partout et on peut toujours comparer deux valuations. Tu penses peut-être au défaut d'antisymétrie ? Auquel cas sauf erreur la question est réglée en se rabattant sur l'ordre usuel quand les valuations sont égales.

[chombier]

Ca a l'air de marcher... A vérifier quand même. Ca sort largement de l'inventaire des solutions que je pouvais imaginer...

J'ai trouvé une solution très similaire par quelqu'un d'autre (http://nicolas.francois.free.fr/arnaudies.html)

Si on note appelle le ième nombre premier ( ; ; ...) et qu'on s'intéresse à la fonction



Par exemple : car

est bijective, c'est un isomorphisme de groupe entre et

L'ordre lexicographique sur est compatible avec l'addition, et induit donc un ordre sur

Pour résumer,  

[aviateur]

Bonsoir
Merci pour le lien mais on demande un pwd.
Sinon l'exemple me semble bien mais il reste à voir que ce groupe n'est pas isomorphe au groupe usuel.

[chombier]

Oui, les fichiers ne sont pas accessibles, le responsable m'a envoyé un mini pdf, mais j'ai tout de même voulu citer ma source.

Les deux ordres ne sont pas isomorphes. La preuve étant que n'est pas un groupe archimédien :
Pour tout .

En effet,

[Mimosa]

> skullkid Si on prend par exemple , Comment compares-tu 1 et 5?

[chombier]

> skullkid Si on prend par exemple , Comment compares-tu 1 et 5?

Ca je peux répondre : avec l'ordre défini par skullkid, comme , on compare 1 et 5 avec l'ordre usuel, ainsi .

[Mimosa]

Et toujours avec , comment on compare 9 et 12?