Lim sup dans un ensemble totalement ordonné

[chombier]

Bonjour à tous,

J'ai besoin d'un peu d'aide pour avancer. Je cherche à caractériser le fait qu'un élément L est inférieur, supérieur, inférieur ou égal, ou supérieur ou égal à la limite supérieure d'une suite.

J'ai décidé de me placer un cas assez général, à savoir un espace totalement ordonné .

Voici mes résultats les plus probants :






---------------- Explications ----------------

J'ai déjà quelques résultats sur les bornes inférieures et les bornes supérieures.

Soit un sous ensemble de E possédant une borne supérieure , c'est à dire un élément de E vérifiant :
BS1 : sup X est un majorant de X
BS2 : quel que soit , si M est un majorant de X alors

J'ai alors montré les résultats suivants : pour tout
est un majorant de X
n'est pas un majorant de X
n'est pas un majorant de X
est un majorant de X

J'ai utilisé un résultat qui est vrai sur n'importe quel ensemble totalement ordonné :


Pour la limite sup, j'ai maintenant une suite à valeurs dans E. Je pose :





Je suppose que cet suite a une limite supérieure, donc que les inf et sup existent. Je cherche à caractériser le fait qu'un élément soit plus grand ou plus petit que cette limite, comme je l'ai fait pour les bornes supérieures :

Soit










Impossible d'obtenir quelque chose de plus explicite.

Est-ce que quelqu'un aurait une idée ? Est-ce que je dois prendre des hypothèse supplémentaires ? Est-ce que vous avez une caractérisation plus propre ?

Si je continue :

[aviateur]

Bonjour
D'abord je ne comprends pas l'intérêt d'écrire une liste aussi exhaustive de formulations équivalentes pour exprimer qu'un élément domine un autre, même si cet autre est une limite sup.
Pour le raisonnement en général, on exhibe la formulation qui va le mieux au raisonnement, et puis c'est tout!
Mais ceci étant dit, ce qui m'interroge , c'est ce que tu dis juste après "je pose...".

=... et

Mais tu es certain que existe toujours?

Et puis après

C'est une égalité entre 2 être mathématiques dont l'existence est questionable et c'est important d'y répondre avant tout ce qui est écrit par la suite.

Il faudrait expliciter cela car tu te places dans un cadre général. Pourquoi pas! Mais il faut gérer.

[chombier]

Bonjour

Tout d'abord merci pour ta réponse.

La liste d'équivalences est censée être plus ou moins une démonstration, en tout cas personellement j'ai besoin de ces étape pour me convaincre que la dernière ligne est vraie !

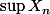
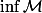
En ce qui concerne les et , il n'y a aucune raison qu'ils existent a priori, je pars donc du principe qu'ils existent, ce qui me permet de parler de lim sup (sinon elle n'existe pas).

Quand à ma démarche, elle pars de là : https://fr.wikiversity.org/wiki/S%C3%A9 ... s_positifs
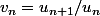
Où il est annoncé (dans le paragraphe sur la règle de D'Alembert, (avec ) que :

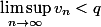
si alors (v_n) est majorée par q à partir d'un certain rang.
Ce qui ne me parait pas si évident de prime abord.

Je me suis posé plusieurs questions :
1) Est-ce vrai car nous travaillons dans R, ou est-ce qu'un ensemble totalement ordonné et une suite qui possède une limite sup ont la même propriété ?
2) La réciproque est-elle vraie ?
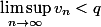
3) si elle ne l'est pas, comment obtenir une équivalence, autrement dit quelle information me donne exactement l'égalité sur la suite (v_n) ?

Voici mes conclusions :

1) C'est vrai dans n'importe quel ensemble totalement ordonné et une suite qui possède une limite sup.
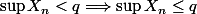
et
2) La réciproque est fausse. Exemple : (u_n) constante égale 0, (u_n) est majorée par 0 à partir du rang 0 et pourtant il est faux d'écrire
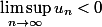
3) L'équivalence est :

(On constate que si la suite est majorée par B, elle est a fortiori majorée par q)

Pourquoi je me place dans le cadre le plus général possible ? Parce qu'il y a des affirmations qu'on utilise très souvent avoir conscience du fait qu'elles utilisent des propriétés intrinsèques à R, par exemple :

Si M est un majorant de , alors M est la borne supérieure de X si et seulement si :
(1)
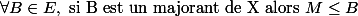
(2)
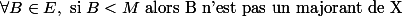
(3)
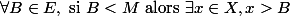
(4)
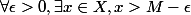
(5)

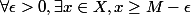
La première affirmation est vraie dans le cas le plus général : celle où E est un ensemble partiellement ordonné. Plus on descends, plus on suppose de choses sur E. Elles sont toutes vraies dans R.

Pour la (2) et la (3), il faut que E soit totalement ordonné
Pour la (4), il faut que E soit un groupe ordonné
Pour la (5), il faut que E soit un groupe ordonné ne possédant pas de plus petit élément.

Peut-être que tout cela n'est pas utile, mais cela me satisfait de savoir de quelles hypothèses j'ai besoin, au minimum, pour affirmer une assertion. Surtout quand je travaille dans R.

[chombier]

J'ai trouvé ce que je cherchais, enfin !

La solution se trouve là dedans : dans on peut caractériser de différentes façons le fait que M <= sup X :

Dans un ensemble totalement ordonné quelconque :



Dans , on a en plus les équivalences suivantes :




Cela permet de simplifier deux équivalences :

Dans un ensemble totalement ordonné quelconque :





Dans , on a en plus les équivalences suivantes :




On voit que dans , la caractérisation du fait qu'un réel soit supérieur ou égal à la limite supérieure d'une suite est plus simple à exprimer que dans un ensemble totalement ordonné quelconque.