Bonjour, notre prof nous a donné cet exo sauf que l'on a juste vu la definition d'un sous espace affine et je n'arrive pas à le faire.
Soit A un sous ensemble de R^3 d'équation x + 2y - 3 z = 5 et B celui d'équations x+y = 3 et x-y-z = 2
Montrer que A et B sont des sous espace affines de R^3.
Quelles en sont leur directions et leur dimension respectives ?
Alors je sais la def d'un sous espace affine :
On appelle sous-espace affine passant a;)E et dirigé par F sous-espace vectoriel E l'ensemble
V=a+F={a+x/x;)F}
Mais je n'arrive pas à l'appliquer,Merci par avance
Geometrie sous espace affine
9 messages
- Page 1 sur 1
Mulan a écrit:Bonjour, notre prof nous a donné cet exo sauf que l'on a juste vu la definition d'un sous espace affine et je n'arrive pas à le faire.
Soit A un sous ensemble de R^3 d'équation x + 2y - 3 z = 5 et B celui d'équations x+y = 3 et x-y-z = 2
Montrer que A et B sont des sous espace affines de R^3.
Quelles en sont leur directions et leur dimension respectives ?
Alors je sais la def d'un sous espace affine :
On appelle sous-espace affine passant a;)E et dirigé par F sous-espace vectoriel E l'ensemble
V=a+F={a+x/x;)F}
Mais je n'arrive pas à l'appliquer,Merci par avance
Bj
x + 2y -3z = 0 est l"équation d'un plan vectoriel F de R^3
a = (5,0,0) est un point de A (on peut en prendre un autre ça change rien)
Montre que A = a + F
Salut : :happy3:
On a :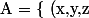 \in \mathbb{R}^{3} \ / \ x+2y-3z -5 = 0 \} $)
On a : \in A $) , car :
, car : 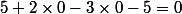
Donc, on a :
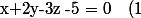 $) et
et 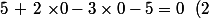 $) deux équations.
deux équations.
On fait la différence de ces deux équations : $) et
et  $) , on obtient :
, on obtient :
+2(y-0)-3(z-0) = 0 $)
C'est à dire : \in \ker f $) , avec
, avec  = x+2y-3z $) ( Une forme linéaire, c'est à dire, un hyperplan )
( Une forme linéaire, c'est à dire, un hyperplan )
C'est à dire : - (5,0,0) \in \ker f $) , c'est à dire :
, c'est à dire :  \in ( 5,0,0) + \ker f $)
Par conséquent : + \ker f $)
Il reste à montrer l'inclusion inverse : + \ker f \subset A $)
Soit \in (5,0,0) + \ker f $) ,alors
,alors  \in \ker f $) , c'est à dire :
, c'est à dire : +2(y-0)-3(z-0) = 0 $) , c'est à dire :
, c'est à dire : 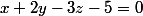
C'est à dire : \in A $)
Conclusion :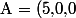 + \ker f $)
Tu fais la même chose pour .
.
Cordialement. :happy3:
Edit : Grillé par Maxmau. :hum: :dodo:
On a :
On a :
Donc, on a :
On fait la différence de ces deux équations :
C'est à dire :
C'est à dire :
Par conséquent :
Il reste à montrer l'inclusion inverse :
Soit
C'est à dire :
Conclusion :
Tu fais la même chose pour
Cordialement. :happy3:
Edit : Grillé par Maxmau. :hum: :dodo:
Bonjour : :happy3:
On a :
 \in \mathbb{R}^{3} \ / \ x+y -3 = 0 \ \mathrm{et} \ x-y-z-2 = 0 \} $)
 \in \mathbb{R}^{3} \ / \ x+y-3 = 0 \} \bigcap \{ (x,y,z) \in \mathbb{R}^{3} \ / \ x-y-z-5 =0 \} = L_1 \bigcap L_2 $) .
.
avec :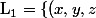 \in \mathbb{R}^{3} \ / \ x+y-3 = 0 \} $) et
et 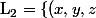 \in \mathbb{R}^{3} \ / \ x-y-z-5 =0 \} $)
En science de la logique, le mot :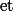 se traduit par :
se traduit par : 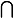 .
.
Voici les étapes à suivre :
 $) Tu trouves d'abord, un point commun
Tu trouves d'abord, un point commun  à
à 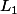 et
et 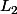 en résolvant le système qui en découle.
en résolvant le système qui en découle.
 $) Tu fais comme j'ai fait pour
Tu fais comme j'ai fait pour  , tu écris :
, tu écris : 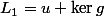 et
et 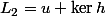 , avec
, avec  et
et  à déterminer.
à déterminer.
 $) Tu déduis comment s'écrit
Tu déduis comment s'écrit  en fonction de
en fonction de  ,
, 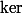 et
et 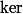 .
.
Cordialement. :happy3:
On a :
avec :
En science de la logique, le mot :
Voici les étapes à suivre :
Cordialement. :happy3:
DM pistes
Bonjour,
Serait-il possible d'avoir de l'aide pour un DM de géométrie affine svp
Merci de votre réponse
Bonne soirée
Serait-il possible d'avoir de l'aide pour un DM de géométrie affine svp
Merci de votre réponse
Bonne soirée
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
