Frontière et adhérence

[Pseuda]

Oui, mais je reviens à ma question : quand on parle de l'adhérence d'une partie, faut-il préciser dans quel evn on se place : l'adhérence peut ne pas être la même si on se place dans R ou dans C ? Exemple ? J'ai du mal à voir.

A ce propos, il y a une question que je me pose depuis longtemps : ne pourrait-on pas considérer Q comme un evn sur Q muni de la norme valeur absolue. Dans ce cas, quelle serait l'adhérence de Q dans l'evn Q ? (car il y a des suites de Q qui ne convergent que dans R)

[Pseuda]

Bon je me suis répondue à la 1ère question : non, l'adhérence d'une partie incluse dans R ne peut pas dépasser R, et cela ne change rien qu'on la considère dans R ou dans C, et celle d'une partie non incluse dans R ne peut bien évidemment pas être incluse dans R (cela n'a pas de sens d'en parler dans R). Merci @aviateur.

(Cela doit être du même style pour des evn inclus les uns dans les autres).

[aviateur]

Rebonjour @pseuda
Ta question est intéressante et j'y réponds en espérant être corrigé si je me trompe.
1. Bien entendu, d'une façon générale, si j'ai un ensemble E muni d'une topologie (issue d'une métrique ou pas)
et A une partie de E. Par définition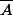 est une partie de E.
Si maintenant j'ai un sur ensemble de E noté F munie aussi d'une topologie, alors, a priori rien n'implique que
l'adhérence de A soit inchangée.
Même si la topologie sur E est celle induite par F.

2. Pour ta question 2, l'adhérence de Q sera Q et d'ailleurs quelque soit la topologie T car Q est un fermé de (Q,T).
Certes (Q,|.|) n'est as complet mais cela n'intervient pas ici.

D'autre part Q comme sous-ensemble de (R,|.|) alors son adhérence est R.

[Ben314]

Si maintenant j'ai un sur ensemble de E noté F munie aussi d'une topologie, alors, a priori rien n'implique que l'adhérence de A soit inchangée.

Concernant cette partie là, il y a quand même un résultat "assez naturel" (valable dans le cas le plus général, c'est à dire celui de la topologie générale) :
Si où E est un espace topologique alors l'adhérence de A vue comme une partie de l'espace topologique F (muni de la topo. induite par celle de E) c'est en fait l'intersection de F avec l'adhérence de A vue comme une partie de E : (et ça se prouve tout bêtement en utilisant le fait que l'adhérence de A, c'est le plus petit fermé contenant A et que les fermés de F pour la topologie induite c'est les traces sur F des fermés de E).
Si on suppose de plus que F est un fermé de E alors c'est encore plus simple vu que dans ce cas et c'est une façon un peu théorique d'expliquer ce que dit pseuda plus haut, à savoir que si tu as une partie A contenue dans un s.e.v. F de E, de calculer l'adhérence de A vu comme une partie de F ou de E, ça change rien (vu que F est fermé dans E).
Attention au fait que ça marche pas du tout pour le calcul de l'intérieur d'une partie A contenue dans un s.e.v. (strict) de E : vue comme une partie de E, l'intérieur de A sera évidement toujours vide vu qu'elle sera contenue dans l'intérieur de F qui est vide (et si ça marche pas, c'est évidement parce qu'un s.e.v., c'est pas une partie ouverte)

[aviateur]

Oui @ben et merci .
Cela ajoute de la précision et cela confirme les réponses données dans les 2exemples.
(remarque on a échangé les rôles de F et E. )

Dans l'exemple 2 avec A=F=Q et E=R, ici F n'est pas un fermé de E et on n' a pas légalité
L'hypothèse F est un fermé est donc essentielle.

Dans l'autre exemple et (avec la topologie associée à la distance naturelle)
F est un fermé de E et on a bien l'égalité

[Pseuda]

Bonjour à tous,

@Mehdi d'accord avec toi, il faut savoir lire entre les lignes, se donner des exemples et des contre-exemples... . Ces théories ne sont pas sorties toutes faites d'un chapeau, mais ont été forgées à l'aide de tâtonnements, d'erreurs, d'exemples, avant de prendre leur forme telle qu'elle nous est présentée.

Concernant Q, pour en revenir aux evn point de départ de ma question, ce que je comprends c'est que Q evn sur Q est fermé (comme tout evn), mais que des suites de rationnels convergentes dans R (comme celle que j'ai donnée plus haut) ne le sont pas dans Q. Une telle suite erre dans Q sans jamais se rapprocher indubitablement d'un rationnel, elle n'est pas convergente. Il n'y a donc pas contradiction avec le fait qu'une partie A de E est fermée ssi toute suite CONVERGENTE de A l'est dans A (ouf).

Pour la 1ère question, mon intuition est donc la bonne.