Forme lineaire surjective
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 12 Déc 2014, 19:12
par adamNIDO » 12 Déc 2014, 19:12
Bonjour,

voila un exemple pour montrer un S.E.A il suffit de lecrire sous S.E.A=Ker (forme lineaire)
mais ma question pour cet est ce qu'ils ont choisir la forme lineare definie par x+y+z+1 ou bien x+y+z de plus pouvez vous me rappel de cours concernant une application surjetive pourqoi f-1(-1)different de ensemble vide pourquoi ils ont pris -1 de pllus est ce que si on a une forme lienairenon nulle implique qu'il est surjective
je sais pas le thoerem de rang dans le dimension finie DimR3=dimKerf+rang or rang=dimImf=dimR car surjective ce qui preuve la dimde Ker f =2
merci pour votre aide
-
zaidoun
- Membre Relatif
- Messages: 179
- Enregistré le: 27 Juil 2013, 16:41
-
 par zaidoun » 12 Déc 2014, 19:23
par zaidoun » 12 Déc 2014, 19:23
En dimension finie:
1) une forme linéaire f: E -->R non nulle est surjective en fait Im(f) est inculs dans R, donc dim (Im(f)<=1 càd égale à 0 ou 1, or f est non nulle donc dim(Im(f))=1=dim(R), par suite Im(f)=R.
2) Théorème du rang: f:E--->F application linéaire alors dim(E)= dim(ker(f)) + rg(f)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 12 Déc 2014, 19:23
par zygomatique » 12 Déc 2014, 19:23
salut
une forme linéaire est par définition linéaire !!!
(x, y, z) --> x + y + z + 1 est-elle linéaire ?
par ailleurs x + y + z + 1= 0 <==> x + y + z = -1
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 12 Déc 2014, 19:27
par adamNIDO » 12 Déc 2014, 19:27
zaidoun a écrit:En dimension finie:
1) une forme linéaire f: E -->R non nulle est surjective en fait Im(f) est inculs dans R, donc dim (Im(f)F application linéaire alors dim(E)= dim(ker(f)) + rg(f)
merci beaucoup mais pourquoi ils ont dit -1 et ils ont dit que f-1(-1) est non vide et pourquoi P=ker f-1(-1)
je pense qu'on doit ecrire P=ker f avce f(x,y,z)=x+y+z-1
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 12 Déc 2014, 19:29
par adamNIDO » 12 Déc 2014, 19:29
zygomatique a écrit:salut
une forme linéaire est par définition linéaire !!!
(x, y, z) --> x + y + z + 1 est-elle linéaire ?
par ailleurs x + y + z + 1= 0 x + y + z = -1
...
Bonjour monsieur
merci beaucoup je pense qu'il est lineaire de plus mais meme question pour vouspourquoi ils ont dit -1 et ils ont dit que f-1(-1) est non vide et pourquoi P=ker f-1(-1)
je pense qu'on doit ecrire P=ker f avce f(x,y,z)=x+y+z-1

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 12 Déc 2014, 19:31
par zygomatique » 12 Déc 2014, 19:31
je t'ai répondu pourquoi ils ont mis -1 ....
pour la question de linéarité, notons f l'application
a-t-on ::
f(0) = 0 ?
f(u + v) = f(u) + f(v) ?
f(ku) = kf(u) ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 12 Déc 2014, 19:33
par adamNIDO » 12 Déc 2014, 19:33
zygomatique a écrit:je t'ai répondu pourquoi ils ont mis -1 ....
pour la question de linéarité, notons f l'application
a-t-on ::
f(0) = 0 ?
f(u + v) = f(u) + f(v) ?
f(ku) = kf(u) ?
donc il y a faute de frappe car ils ont considere f(x,y,z)=x+y+z et pas x+y+z-1
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 12 Déc 2014, 19:34
par adamNIDO » 12 Déc 2014, 19:34
zygomatique a écrit:je t'ai répondu pourquoi ils ont mis -1 ....
pour la question de linéarité, notons f l'application
a-t-on ::
f(0) = 0 ?
f(u + v) = f(u) + f(v) ?
f(ku) = kf(u) ?
donc il y a faute de frappe car ils ont considere f(x,y,z)=x+y+z et pas x+y+z-1
f(0)=-1 donc la forme x+y+z-1 nest pas forme lineaire nest ce pas monsieur
-
zaidoun
- Membre Relatif
- Messages: 179
- Enregistré le: 27 Juil 2013, 16:41
-
 par zaidoun » 12 Déc 2014, 19:36
par zaidoun » 12 Déc 2014, 19:36
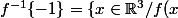=-1\})
et puisque f est surjective donc cet ensemble est non vide.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 12 Déc 2014, 19:39
par adamNIDO » 12 Déc 2014, 19:39
zaidoun a écrit: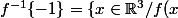=-1\})
et puisque f est surjective donc cet ensemble est non vide.
voila ce que je cherche la caractérisation de

merci beaucoup
cest parce que ils ont mis

donc on peut pas ecrire P sous forme de Ker
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités

