Fonction (parité, injective, surjective)
21 messages
- Page 1 sur 2 - 1, 2
Fonction (parité, injective, surjective)
Bonjour et merci d'avance pour votre aide.
Je dois déterminer si la fonction x^2+(-1)^x est injective et/ou surjective ainsi que sa parité dans N.
Pour la parité je trouve:
f(-x)=-x^2+(-1)^-x=x^2+(-1)^-x
-f(x)=-x^2-(-1)^x=x^2-(-1)^x
donc ni paire ni impaire
j'ai corrigé.
pour f(x) est elle injective?
f(x')=f(x) ?
j'obtient:
x'^2-x^2=(-1)^x'+(-1)^x
et à ce niveau là je me demande si je dois préciser si x et/ou x' sont pair et/ou impair?
pour f(x) est elle surjective
je pose y=f(x) mais je ne sais pas trop dans qu'elle direction aller...
Je dois déterminer si la fonction x^2+(-1)^x est injective et/ou surjective ainsi que sa parité dans N.
Pour la parité je trouve:
f(-x)=-x^2+(-1)^-x=x^2+(-1)^-x
-f(x)=-x^2-(-1)^x=x^2-(-1)^x
donc ni paire ni impaire
j'ai corrigé.
pour f(x) est elle injective?
f(x')=f(x) ?
j'obtient:
x'^2-x^2=(-1)^x'+(-1)^x
et à ce niveau là je me demande si je dois préciser si x et/ou x' sont pair et/ou impair?
pour f(x) est elle surjective
je pose y=f(x) mais je ne sais pas trop dans qu'elle direction aller...
tu fais une erreur de calculs dans ton -f(x) (une histoire de parenthèse est en cause je pense)
Et si c'est défini sur N l'ensenmble de définition n'étant pas symétrique, pas la peine d'étudier la parité...
Et si c'est défini sur N l'ensenmble de définition n'étant pas symétrique, pas la peine d'étudier la parité...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Salut,
Vu que tu est parti à étudier l'équation f(x)=y (où y est fixé est l'inconnue est x), tant qu'à faire, sert t'en à la fois pour la surjectivité ET l'injectivité :
- f surjective <=> cette équation a toujours au moins une solution (quelque soit le y)
- f injective <=> cette équation a toujours au plus une solution (quelque soit le y)
Aprés, pour résoudre l'équation, il me semble que tu es obligé de distinguer 2 cas : x pair / x impair.
P.S. D'attaquer "bille en tète" à regarder l'injectivité et la surjectivité avec la définition ne me semble pas le plus malin dans un exo de ce type où la fonction est définie sur N.
Perso, j'aurais commencé par calculer les images des premiers entiers 0,1,2,3,4 "pour voir..."
Vu que tu est parti à étudier l'équation f(x)=y (où y est fixé est l'inconnue est x), tant qu'à faire, sert t'en à la fois pour la surjectivité ET l'injectivité :
- f surjective <=> cette équation a toujours au moins une solution (quelque soit le y)
- f injective <=> cette équation a toujours au plus une solution (quelque soit le y)
Aprés, pour résoudre l'équation, il me semble que tu es obligé de distinguer 2 cas : x pair / x impair.
P.S. D'attaquer "bille en tète" à regarder l'injectivité et la surjectivité avec la définition ne me semble pas le plus malin dans un exo de ce type où la fonction est définie sur N.
Perso, j'aurais commencé par calculer les images des premiers entiers 0,1,2,3,4 "pour voir..."
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Par contre, il faut ABSOLUMENT que ça soit clair en ce qui concerne l'ensemble de départ et d'arrivé de ton aplication : si f est une application de A dans B, l'injectivité de f dépend fortement de A (mais pas vraiment de B, pourvu que çe soit cohérent) et la surjectivité dépend fortement de A et de B...
Donc, ta fonction, c'est quoi EXACTEMENT son ensemble de départ et son ensemble d'arrivé ?
Donc, ta fonction, c'est quoi EXACTEMENT son ensemble de départ et son ensemble d'arrivé ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
merci pour vos réponses! L'ensemble de la fonction est N dans N.
Comme dit plus haut pas besoin de vérifier la parité puisque l'on travaille dans N. Cependant juste pour le faire je trouve f(x)=f(-x) grâce à (-1)^x = (-1)^-x merci!
f(x) est injective quand le couple (x,x') est pair ou impair.
Pour la surjectivité je me dis que comme x^2+(-1)^x donnera toujours un entier nul ou positif f(x) est surjective. Mais est ce suffisant pour le prouver?
Comme dit plus haut pas besoin de vérifier la parité puisque l'on travaille dans N. Cependant juste pour le faire je trouve f(x)=f(-x) grâce à (-1)^x = (-1)^-x merci!
f(x) est injective quand le couple (x,x') est pair ou impair.
Pour la surjectivité je me dis que comme x^2+(-1)^x donnera toujours un entier nul ou positif f(x) est surjective. Mais est ce suffisant pour le prouver?
Sans regarder plus loin, ça :
- Déja ce qui est injecif (ou pas), c'est une fonction et f(x), c'est pas une fonction, c'est un entier (qui dépend de x).
La fonction elle s'appelle f (tout seul) ou alors tu écrit soit x->f(x) : la fonction qui à x associe f(x). (ça semble pédant comme remarque, mais si tu écrit que la fonction c'est f(x), ça te conduit imencablement à écrire le style d'annerie çi dessus)
- Le fait qu'une fonction f soit (ou pas) injective, ça ne risque pas de dépendre de x. Soit elle l'est, soit... elle ne l'est pas, un point c'est tout. C'est là qu'on voit l'importance de ne JAMAIS écrire "la fonction f(x).
A la limite elle peut changer de status (injective ou pas) en fonction de l'ensemble de départ choisi, par exemple la fonction x->x^2 (et pas la fonction x² !!!) est injective SUR R+ mais n'est pas injective SUR R
- "Le couple (x,x') est pair ou impair", je vois franchement pas non plus ce que ça veut dire...
Et, en regardant plus loin... :doh: , ça :
Ce que tu raconte, c'est que pour un x donné on peut toujours calculer f(x) : ça n'a absolument rien à voir avec la définition de "surjectif".
En fait, c'est la définition d'une application : pour n'importe quel x de l'ensemble de départ, il y a un et un seul f(x) dans l'ensemble d'arrivé. Et comme là, à mon avis, l'exo commence par "Soit f l'application blablabla", tu as rien montré du tout.
Quand on se pose la question de l'injectivité et de la surjectivité, c'est exactement l'inverse qu'on fait : on fixe un élément y de l'ensemble d'arrivé et on regarde s'il y a un ou des x de l'ensemble de départ qui lui correspond (i.e. des x vérifiant f(x)=y)
- Si, quelque soit le y, il y a au moins un x, on dit qu'elle est surjective.
- Si, quelque soit le y, il y a au plus un x (donc zéro ou un), on dit qu'elle est injective.
- Si, quelque soit le y, il y a exactement un x on dit qu'elle est bijective et, dans ce cas, l'application qui à y associe le x est appellée "bijection réciproque".
Donc ici, si on prend "stricto senso" les définitions, pour regarder si f est injective/surjective, on prend un élément y de l'ensemble d'arrivé (donc un y dans N) et on cherche s'il y a des x de l'ensemble de départ (donc aussi N) tel que f(x)=y.
Ca revient à écrire^x=y\) que tu regarde comme une équation où y est connu et c'est x qu'on cherche.
que tu regarde comme une équation où y est connu et c'est x qu'on cherche.
Et, de nouveau, comme l'ensemble de départ est N, je te réinsite à faire un tableau avec les premières valeurs de la fonction f :
x = 0 , 1 , 2 , 3 , 4
f(x) = ? , ? , ? , ? , ?
ce qui risque de te permettre de conjecturer les réponses (injectif ? surjectif ?)
ça ne veut ABSOLUMENT rien dire :Sei a écrit:f(x) est injective quand le couple (x,x') est pair ou impair.
- Déja ce qui est injecif (ou pas), c'est une fonction et f(x), c'est pas une fonction, c'est un entier (qui dépend de x).
La fonction elle s'appelle f (tout seul) ou alors tu écrit soit x->f(x) : la fonction qui à x associe f(x). (ça semble pédant comme remarque, mais si tu écrit que la fonction c'est f(x), ça te conduit imencablement à écrire le style d'annerie çi dessus)
- Le fait qu'une fonction f soit (ou pas) injective, ça ne risque pas de dépendre de x. Soit elle l'est, soit... elle ne l'est pas, un point c'est tout. C'est là qu'on voit l'importance de ne JAMAIS écrire "la fonction f(x).
A la limite elle peut changer de status (injective ou pas) en fonction de l'ensemble de départ choisi, par exemple la fonction x->x^2 (et pas la fonction x² !!!) est injective SUR R+ mais n'est pas injective SUR R
- "Le couple (x,x') est pair ou impair", je vois franchement pas non plus ce que ça veut dire...
Et, en regardant plus loin... :doh: , ça :
c'est pas mieux.Sei a écrit:Pour la surjectivité je me dis que comme x^2+(-1)^x donnera toujours un entier nul ou positif f(x) est surjective.
Ce que tu raconte, c'est que pour un x donné on peut toujours calculer f(x) : ça n'a absolument rien à voir avec la définition de "surjectif".
En fait, c'est la définition d'une application : pour n'importe quel x de l'ensemble de départ, il y a un et un seul f(x) dans l'ensemble d'arrivé. Et comme là, à mon avis, l'exo commence par "Soit f l'application blablabla", tu as rien montré du tout.
Quand on se pose la question de l'injectivité et de la surjectivité, c'est exactement l'inverse qu'on fait : on fixe un élément y de l'ensemble d'arrivé et on regarde s'il y a un ou des x de l'ensemble de départ qui lui correspond (i.e. des x vérifiant f(x)=y)
- Si, quelque soit le y, il y a au moins un x, on dit qu'elle est surjective.
- Si, quelque soit le y, il y a au plus un x (donc zéro ou un), on dit qu'elle est injective.
- Si, quelque soit le y, il y a exactement un x on dit qu'elle est bijective et, dans ce cas, l'application qui à y associe le x est appellée "bijection réciproque".
Donc ici, si on prend "stricto senso" les définitions, pour regarder si f est injective/surjective, on prend un élément y de l'ensemble d'arrivé (donc un y dans N) et on cherche s'il y a des x de l'ensemble de départ (donc aussi N) tel que f(x)=y.
Ca revient à écrire
Et, de nouveau, comme l'ensemble de départ est N, je te réinsite à faire un tableau avec les premières valeurs de la fonction f :
x = 0 , 1 , 2 , 3 , 4
f(x) = ? , ? , ? , ? , ?
ce qui risque de te permettre de conjecturer les réponses (injectif ? surjectif ?)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Sei a écrit:
Pour la surjectivité je me dis que comme x^2+(-1)^x donnera toujours un entier nul ou positif f(x) est surjective. Mais est ce suffisant pour le prouver?
Essaie de voir s'il existe un entier n tel que f(n)=2
On peut aussi montrer que f(n+1)>f(n) si n>0, ce qui peut aider pour l'injectivité
Pour résumer:
f de N dans N définie par f(x)=x^2+(-1)^x
Elle n'est ni paire ni impaire puisque définie dans N.
Juste pour le calcul je trouve f(x)=f(-x) quelqu'un peut me confirmer?
x: 1;2;3;4;5
f(x):1;0;5;8;17;24
Elle n'est pas bijective puisque f(x)=2 n'a pas de solution dans N.
Peut on résoudre ce problème par calcul?
Au vu du tableau elle est injective puisque quelque soit y il y a une solution.
Par calcul f(x')=f(x) ?
J'obtient x'²-x²=-(-1)^x'+(-1)^x
Et là je croyais que je devais différencié si x et x' sont pair ou impair car avec les puissances si x et x' sont pair ou impair tout les 2 on obtient bien x'²-x²=0 donc x'²=x² donc x'=x
f de N dans N définie par f(x)=x^2+(-1)^x
Elle n'est ni paire ni impaire puisque définie dans N.
Juste pour le calcul je trouve f(x)=f(-x) quelqu'un peut me confirmer?
x: 1;2;3;4;5
f(x):1;0;5;8;17;24
Elle n'est pas bijective puisque f(x)=2 n'a pas de solution dans N.
Peut on résoudre ce problème par calcul?
Au vu du tableau elle est injective puisque quelque soit y il y a une solution.
Par calcul f(x')=f(x) ?
J'obtient x'²-x²=-(-1)^x'+(-1)^x
Et là je croyais que je devais différencié si x et x' sont pair ou impair car avec les puissances si x et x' sont pair ou impair tout les 2 on obtient bien x'²-x²=0 donc x'²=x² donc x'=x
OuiSei a écrit:Elle n'est ni paire ni impaire puisque définie dans N.
incohérent vu l'énoncé : on ne peut (quasiment) jamais avoir à la fois x et -x dans l'ensemble de départ N de la fonction f.Sei a écrit:...je trouve f(x)=f(-x)...
tu en déduit plus précisément qu'elle n'est pas surjective (donc forcément pas bijective)Sei a écrit:Elle n'est pas bijective puisque f(x)=2 n'a pas de solution dans N.
Façilement : siSei a écrit:Peut on résoudre ce problème par calcul?
- Soit
- Soit
pas clair : une solution à quoi ? et si la réponse est "une solution à l'équation f(x)=y" alors c'est faux : tu vient d'écrire 2 lignes au dessus que, lorsque y=2, il n'y avait pas de solution à l'équation f(x)=y:mur:Sei a écrit:...elle est injective puisque quelque soit y il y a une solution.
En plus, pour l'injectivité, ce qu'il faut montrer, c'est qu'il y a AU PLUS une solution, donc s'il n'y a pas de solution, c'est O.K. (il faudrait quand même que tu lise ce qu'on te répond : ça, ça fait la 3em ois que je te l'écrit !!!)
Pas clair non plus sur la démarche : IL FAUT APPRENDRE A REDIGER.Sei a écrit:Par calcul f(x')=f(x) ?
J'obtient x'²-x²=-(-1)^x'+(-1)^x
Et là je croyais que je devais différencié si x et x' sont pair ou impair car avec les puissances si x et x' sont pair ou impair tout les 2 on obtient bien x'²-x²=0 donc x'²=x² donc x'=x
Il faut ABSOLUMENT que, dans un cas comme ici, tu ecrive EN ENTIER :
"Soient x et x' deux éléments de N (ensemble de départ). On suppose que f(x)=f(x'). Peut-on en déduire que x=x' ?"
sinon, celui qui te lit à l'impression de lire du "charabia" et toi même, au bout de deux ligne, tu y comprend "que dalle" à ce que tu écrit....
Donc je reprend tout ce qui ne va pas (à peu prés tout...) :
Enfin, il faudrait que tu choisisse en ce qui concerne la façon dont tu va montrer l'injectivité : Va tu montrer que tout y du but N admet au plus un antécédent ou bien que deux éléments de l'ensemble de départ ayant la même image sont forcément égaux ?Sei a écrit:Par calcul f(x')=f(x) ?
- On ne sait pas qui sont x et x'.
- On ne sait pas si le fameux f(x)=f(x') c'est un truc que tu supose vrai ou si c'est un truc que tu veut démontrer (et le point d'interogation donne l'impression que c'est ce que tu veut montrer alors qu'en fait c'est ce que l'on doit supposer au départ.
J'obtient x'²-x²=-(-1)^x'+(-1)^x
- Idem : le "j'obtient" est on ne peut plus mal adapté vu que ça, c'est ce que tu suppose
Et là je croyais que je devais différencié si x et x' sont pair ou impair car avec les puissances si x et x' sont pair ou impair tout les 2 on obtient bien x'²-x²=0 donc x'²=x² donc x'=x
- "pas trop faux", sauf qu'il te manque le seul cas intéréssant, c'est à dire celui où x et x' ne sont pas tout les deux de même parité
C'est équivalent (façile à prouver), mais au niveau de la démarche pour la preuve, ce n'est pas tout à fait la même chose...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Elle n'est pas bijective puisque f(x)=2 n'a pas de solution dans N.
Peut on résoudre ce problème par calcul?
Une autre idée : en calculant les premiers f(x) on voit bien que ça croît, donc si on n'a pas eu de f(x)=2 pour les premiers x, c'est fichu. Voici la méthode qui découle de cette idée :
- Pour tout x, on a f(x) >= x²-1 (vu que f(x) vaut soit x²-1, soit x²+1).
- Donc pour tout x >=4, on a f(x) >=15. Ceci prouve qu'aucun entier >=4 n'a pour image 2 (puisque 2 est plus petit que 15).
- Or les entiers 0, 1, 2, 3 et 4 n'ont pas pour image 2 (tu as calculé leurs images, 2 n'est jamais sorti).
- Donc en fait, personne n'a pour image 2.
Bon, c'est plus long que la solution de Ben314...
Bon, je te fait un modèle propre d'une façon de prouver les résultats (pas la plus simple...)
Le truc important et qu'il faut ABSOLUMENT COMPRENDRE, c'est que les phrases, c'est pas de "l'enrobage" des formules mathématiques : c'est elles qui donnent du sens à ce que tu écrit : si tu les met pas on comprend rien (et le "on", il y a de fortes chance que tu soit compris de dans...)
Notre fonction f est définie de N dans N.
Pour voir si elle est injective ou surjective, considérons un élément fixé de l'ensemble d'arrivé N et cherchons ces éventuel(s) antécédent(s), c'est à dire les éventuel(s) x de l'ensemble de départ N tels que :
^x=y)
(là, le "laïus" çi dessus, il doit, au mini, dire que y est un entier naturel connu et que l'on cherche l'entier naturel inconnu x)
- Si x est impair, l'équation se ramène à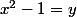 , c'est à dire à
, c'est à dire à 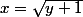 (x doit être positif vu qu'on cherche un entier naturel) mais ce n'est pas forcément une solution vu que
(x doit être positif vu qu'on cherche un entier naturel) mais ce n'est pas forcément une solution vu que 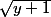 risque de ne pas être un entier impair.
risque de ne pas être un entier impair.
- Si x est pair, l'équation se ramène à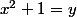 , c'est à dire
, c'est à dire 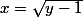 en suposant que le y fixé est supérieur à 1.
en suposant que le y fixé est supérieur à 1.
A priori, il y a donc au maximum deux solution, mais pour qu'il y en ait 2, il faut que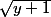 soit un entier impair ET que
soit un entier impair ET que 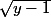 soit un entier pair, c'est à dire que
soit un entier pair, c'est à dire que 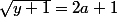 et
et 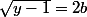 avec
avec  et
et  entiers.
entiers.
La première équation conduit à^2-1=4a(a+1)) qui implique en particulier que le y choisi soit un multiple de 4 alors que la deuxième conduit à
qui implique en particulier que le y choisi soit un multiple de 4 alors que la deuxième conduit à ^2+1=4b^2+1) qui implique que y doit être impair.
qui implique que y doit être impair.
Comme on ne peut avoir les deux en même temps, cela signigie qu'il y a AU PLUS une solution à l'équation=y) c'est à dire que f est injective.
c'est à dire que f est injective.
Concernant la surjectivité, il faut regarder s'il y a AU MOINS une solution quelque soit le y de départ, or pour y=2, la solution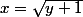 ne va pas vu que ce n'est pas un entier et la solution
ne va pas vu que ce n'est pas un entier et la solution 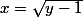 ne va pas non plus vu que ce n'est pas un entier pair.
ne va pas non plus vu que ce n'est pas un entier pair.
Bon, aprés, dans un exo comme celui là, ce n'est pas du tout la meilleure méthode de procéder ainsi.
La meilleure méthode est sans doute celle proposée par chan79, c'est à dire de montrer que f est strictement croissants sur N privé de 0 (résultat qu'on conjecture façilement en regardant le tableau des premières valeur et qui est façile à montrer)
Le truc important et qu'il faut ABSOLUMENT COMPRENDRE, c'est que les phrases, c'est pas de "l'enrobage" des formules mathématiques : c'est elles qui donnent du sens à ce que tu écrit : si tu les met pas on comprend rien (et le "on", il y a de fortes chance que tu soit compris de dans...)
Notre fonction f est définie de N dans N.
Pour voir si elle est injective ou surjective, considérons un élément fixé de l'ensemble d'arrivé N et cherchons ces éventuel(s) antécédent(s), c'est à dire les éventuel(s) x de l'ensemble de départ N tels que :
(là, le "laïus" çi dessus, il doit, au mini, dire que y est un entier naturel connu et que l'on cherche l'entier naturel inconnu x)
- Si x est impair, l'équation se ramène à
- Si x est pair, l'équation se ramène à
A priori, il y a donc au maximum deux solution, mais pour qu'il y en ait 2, il faut que
La première équation conduit à
Comme on ne peut avoir les deux en même temps, cela signigie qu'il y a AU PLUS une solution à l'équation
Concernant la surjectivité, il faut regarder s'il y a AU MOINS une solution quelque soit le y de départ, or pour y=2, la solution
Bon, aprés, dans un exo comme celui là, ce n'est pas du tout la meilleure méthode de procéder ainsi.
La meilleure méthode est sans doute celle proposée par chan79, c'est à dire de montrer que f est strictement croissants sur N privé de 0 (résultat qu'on conjecture façilement en regardant le tableau des premières valeur et qui est façile à montrer)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Pour l'injectivité, j'aurais fait quelque chose de ce genre (ça reprend le début du travail de Sei) :
Soient x et x' deux entiers naturels tels que f(x) = f(x') (E).
- Si x' est de même parité que x, alors (E) est équivalent à x² = x'², ce qui implique que x = x' (et ils sont en effet de même parité).
- Si x' est de parité différente de celle de x, alors (E) est équivalent à |x² - x'²| = 2 (je ne détaille pas, ça vient du fait que si on calcule leur différence, on trouve soit 2, soit -2). Supposons que x >= x'. On a donc :
(E) <==> (x-x')(x+x') = 2 <==> (x-x' = 1 et x+x' = 2) ou (x-x' = 2 et x+x' = 1) .
Le premier cas donne x = x' + 1, donc x + x' = 2 <==> 2x' + 1 = 2 <==> x' = 1/2 : impossible.
Le deuxième cas donne x = x' + 2, donc x + x' = 1 <==> 2x' + 2 = 1 <==> x' = -1/2 : impossible.
Si on suppose x' >= x ça redonne bien sûr la même conclusion (en inversant les rôles de x et x') : (E) est impossible lorsque x et x' sont de parités différentes.
Conclusion : si f(x) = f(x') alors nécessairement x = x'. f est donc injective.
Soient x et x' deux entiers naturels tels que f(x) = f(x') (E).
- Si x' est de même parité que x, alors (E) est équivalent à x² = x'², ce qui implique que x = x' (et ils sont en effet de même parité).
- Si x' est de parité différente de celle de x, alors (E) est équivalent à |x² - x'²| = 2 (je ne détaille pas, ça vient du fait que si on calcule leur différence, on trouve soit 2, soit -2). Supposons que x >= x'. On a donc :
(E) <==> (x-x')(x+x') = 2 <==> (x-x' = 1 et x+x' = 2) ou (x-x' = 2 et x+x' = 1) .
Le premier cas donne x = x' + 1, donc x + x' = 2 <==> 2x' + 1 = 2 <==> x' = 1/2 : impossible.
Le deuxième cas donne x = x' + 2, donc x + x' = 1 <==> 2x' + 2 = 1 <==> x' = -1/2 : impossible.
Si on suppose x' >= x ça redonne bien sûr la même conclusion (en inversant les rôles de x et x') : (E) est impossible lorsque x et x' sont de parités différentes.
Conclusion : si f(x) = f(x') alors nécessairement x = x'. f est donc injective.
Moi j'aurais écrit que, pour tout entier naturel  non nul (ça me gonfle de noter x un entier...)
non nul (ça me gonfle de noter x un entier...)
-f(n)=(n+1)^2+(-1)^{n+1}-n^2-(-1)^n=2n+1-2(-1)^n\geq2n+1-2>0)
Ce qui montre que<f(2)<f(3)<...)
Vu que) est strictement entre
est strictement entre ) et
et ) on en déduit l'injectivité.
on en déduit l'injectivité.
Et pour la non surjectivité, il suffit de prendre un strictement compris entre
strictement compris entre ) et
et 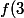) : la croissance de f montre qu'il n'a pas d'antécédent.
: la croissance de f montre qu'il n'a pas d'antécédent.
Ce qui montre que
Vu que
Et pour la non surjectivité, il suffit de prendre un
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
