Problème injective, surjective...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
marie9
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Sep 2008, 19:30
-
 par marie9 » 14 Sep 2008, 16:35
par marie9 » 14 Sep 2008, 16:35
Alors |x|=|x'|
-
COTLOD
- Membre Relatif
- Messages: 104
- Enregistré le: 14 Sep 2008, 10:07
-
 par COTLOD » 14 Sep 2008, 16:37
par COTLOD » 14 Sep 2008, 16:37
Oui, la première composante permet de régler le problème du signe.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 14 Sep 2008, 16:38
par leon1789 » 14 Sep 2008, 16:38
marie9 a écrit:Alors |x|=|x'|
oui, c'est exact ! x = x' ou x = -x'. Là, tu t'es servie de la seconde coordonnée, ok.
Ensuite, que peux-tu ajouter en utilisant la première coordonnée maintenant que tu sais que x=x' ou x=-x' ?
-
marie9
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Sep 2008, 19:30
-
 par marie9 » 14 Sep 2008, 17:10
par marie9 » 14 Sep 2008, 17:10
sin(x)=sin(x') ou sin(x)=sin(-x')

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 14 Sep 2008, 17:16
par leon1789 » 14 Sep 2008, 17:16
marie9 a écrit:sin(x)=sin(x') ou sin(x)=sin(-x')
oui.
Tu connais le lien entre sin(-x') et sin(x') ?
-
marie9
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Sep 2008, 19:30
-
 par marie9 » 14 Sep 2008, 17:24
par marie9 » 14 Sep 2008, 17:24
sin(-x)=pi-sin(x')

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 14 Sep 2008, 17:26
par leon1789 » 14 Sep 2008, 17:26
marie9 a écrit:sin(-x)=pi-sin(x')
heu pourquoi ?
mais il s'agissait du lien entre sin(-
x') et sin(
x').

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 14 Sep 2008, 17:30
par leon1789 » 14 Sep 2008, 17:30
heu pourquoi ?
mais il s'agissait du lien entre sin(-x') et sin(x').
-
marie9
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Sep 2008, 19:30
-
 par marie9 » 14 Sep 2008, 17:34
par marie9 » 14 Sep 2008, 17:34
Désolé j'ai écris n'importe quoi...
sin(-x')=sin(x')

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 14 Sep 2008, 17:36
par leon1789 » 14 Sep 2008, 17:36
marie9 a écrit:sin(-x')=sin(x')
non, pas tout à fait... :triste:
-
marie9
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Sep 2008, 19:30
-
 par marie9 » 14 Sep 2008, 17:42
par marie9 » 14 Sep 2008, 17:42
sin(-x')=-sin(x') ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 14 Sep 2008, 17:44
par leon1789 » 14 Sep 2008, 17:44
marie9 a écrit:sin(-x')=-sin(x') ?
tu es certaine ou pas ?
-
marie9
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Sep 2008, 19:30
-
 par marie9 » 14 Sep 2008, 17:53
par marie9 » 14 Sep 2008, 17:53
OUI ... :id:

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 14 Sep 2008, 18:01
par leon1789 » 14 Sep 2008, 18:01
bon ok, résumons :
-- si x=x' alors
 = sin(x'))
-- si
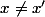
alors
 = -sin(x') \neq sin(x'))
Une de ces deux lignes n'est pas cohérente avec h(x)=h(x'). Laquelle ? Et conclusion ?
-
marie9
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Sep 2008, 19:30
-
 par marie9 » 14 Sep 2008, 18:01
par marie9 » 14 Sep 2008, 18:01
C'est pas ça ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 14 Sep 2008, 18:06
par leon1789 » 14 Sep 2008, 18:06
ok, résumons :
* on a x=x' ou x=-x'
* on a sin(x)=sin(x')
** si x=x' alors sin(x)=sin(x')
** si x=-x' alors sin(x)=sin(-x')=-sin(x')
Notre hypothèse est que sin(x)=sin(x'). Donc ....
-
marie9
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Sep 2008, 19:30
-
 par marie9 » 14 Sep 2008, 18:06
par marie9 » 14 Sep 2008, 18:06
Je ne comprends pas ce que tu as écris sur la deuxième ligne : sinon sin(x) = -sin(x') \neq sin(x')
-
marie9
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Sep 2008, 19:30
-
 par marie9 » 14 Sep 2008, 18:08
par marie9 » 14 Sep 2008, 18:08
x=x' et h est injective

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 14 Sep 2008, 18:12
par leon1789 » 14 Sep 2008, 18:12
marie9 a écrit:x=x'
pourquoi ?
-
marie9
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Sep 2008, 19:30
-
 par marie9 » 14 Sep 2008, 18:17
par marie9 » 14 Sep 2008, 18:17
on a sin(x)=sin(x')
alors x=x'
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
