Fonctions numériques (injection, surjection)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anonyme
par Anonyme » 09 Nov 2005, 18:04
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
par becirj » 09 Nov 2005, 19:50
Bonsoir
1. Soit
,
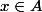
\in f(A))
))
est l'ensemble des éléments de E qui ont une image dans
)
donc
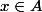
d'où l'inclusion.
Soit
))
alors
)
avec
)
\in B)
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
par becirj » 09 Nov 2005, 20:20
Première équivalence
Soit f injective il faut démontrer que
)\subset A)
Soit
))
alors
\in f(A))
)
donc il existe
tel que
)
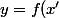. Or f est injective donc
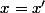
d'où
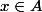
Réciproquement : Soit x et x' appartenant à E tels que
=f(x'))
=f^{-1}f(\{x'\}))
soit
d'où
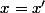
. f est donc injective
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
par becirj » 09 Nov 2005, 20:31
Deuxième équivalence
Soit f surjective. Il faut montrer que
))
Soit
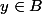
. Comme f est surjective, il existe
tel que
=y)
et
\in f(f^{-1}(B)))
d'où l'inclusion cherchée;
Réciproquement :
=F)
or
\subset E)
soit
)
. Par conséquent
=F)
et f est surjective.
-
Anonyme
par Anonyme » 09 Nov 2005, 20:41
Merci de cette réponse! Je vais de ce pas étudier tout cela ... bonne soirée! ^^
-
Anonyme
par Anonyme » 09 Nov 2005, 21:32
becirj a écrit:Première équivalence
Soit f injective il faut démontrer que
>> N'est-ce pas plutôt une "égalité" à démontrer au lieu de cette inclusion...?
-
danskala
- Membre Relatif
- Messages: 129
- Enregistré le: 06 Mai 2005, 16:48
-
par danskala » 09 Nov 2005, 22:17
salut,
Pour montrer
))
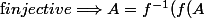il suffit de montrer que
car tu as montré à la question 1°) que
))
pour toute partie A et pour toute fonction f.
bye
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Un peu d'aide serait la bienvenue... merci d'avance