Salut,
Pour la question a), effectivement, si tu prend une courbe qui oscille de plus en plus vite entre la droite y=0 et la courbe d'une fonction positive qui tend vers 0, ça te donnera un contre exemple.
Comme fonction positive qui tend vers 0, la première qui vient à l'esprit, c'est
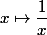
(*) et, comme fonction qui oscille, la première qui vient à l'esprit, c'est la fonction sinus (ou cosinus). Sauf qu'elle oscille entre -1 et 1 donc pour avoir quelque chose de positif, il faut ajouter 1.
Et ça te dit qu'un truc qui devrait marcher, c'est
}{x})
où le

est là pour que ça oscille de plus en plus vite.
Sinon, concernant le b), c'est de nouveau faux : imagine une fonction (quasi) constante sur de larges intervalles mais qui descend de façon très soudaine (et pendant très peu de temps) pour passer d'un intervalle au suivant.
Après, je sais pas si c'est facile d'en trouver une sous la forme d'une unique formule
\!=\!...)
, mais en la définissant "par cas", c'est élémentaire.
(*) Si tu veut que la fonction soit définie sur R tout entier, tu peut prendre à la place
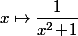
voire même
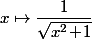
si tu veut avoir exactement le même comportement que
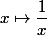
en

. De toute façon, ça changera pas grand chose aux arguments qui suivent.
