Factorisation de a^n-b^n
19 messages
- Page 1 sur 1
Factorisation de a^n-b^n
Bonjour, je travaille en ce moment avant d'entrer en PCSI en septembre et je suis tombé sur une formules dont je ne comprend pas la provenance. Jai fait pas mal de recherche, plein d'autres forums en parlent mais je n'arrive pas à comprendre comment on passe de l'un à l'autre:
a^n-b^n = (a-b)(a^{n-1}+ba^{n-2}+b^2a^{n-3}+...+b^{n-2}a+b^{n-1})
C'est pas très clair comme ça, ça le serais plus avec une somme mais je ne sais pas comment les faire avec un ordi :ptdr:
a^n-b^n = (a-b)(a^{n-1}+ba^{n-2}+b^2a^{n-3}+...+b^{n-2}a+b^{n-1})
C'est pas très clair comme ça, ça le serais plus avec une somme mais je ne sais pas comment les faire avec un ordi :ptdr:
Salut !
- Supposons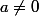 ; montrer que
; montrer que 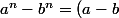(a^{n-1}+ba^{n-2}+b^2a^{n-3}+\cdots +b^{n-2}a+b^{n-1})) revient donc à montrer que :
revient donc à montrer que :
[CENTER]^{n} = \left(1-\frac{b}{a} \right) \left( (1+\frac{b}{a}+\left( \frac{b}{a} \right)^2 +...+\left( \frac{b}{a} \right)^{n-2} +\left( \frac{b}{a} \right)^{n-1} \right)) [/CENTER]
[/CENTER]
Ensuite, en remarquant que^2 +...+\left( \frac{b}{a} \right)^{n-2} +\left( \frac{b}{a} \right)^{n-1}) est la somme de
est la somme de  termes consécutifs d'une suite géométrique déduis-en la valeur de cette somme et donc ton résultat.
termes consécutifs d'une suite géométrique déduis-en la valeur de cette somme et donc ton résultat.
- Montre que cette égalité reste vraie lorsque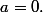
- Supposons
[CENTER]
Ensuite, en remarquant que
- Montre que cette égalité reste vraie lorsque
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
C'est quand meme l'oeuf avant la poule, ou la poule avant l'oeuf de passer par la somme d'une progression geometrique pour déduire la formule de l'énoncé.
Il suffit de developper le membre de droite pour arriver tout de suite sur le membre de gauche.
Les a.a^ib^(n-i-1) se tuent avec les -b.a^(i+1)b^{n-i-2}, il ne reste que les termes a^n et b^n.
Il suffit de developper le membre de droite pour arriver tout de suite sur le membre de gauche.
Les a.a^ib^(n-i-1) se tuent avec les -b.a^(i+1)b^{n-i-2}, il ne reste que les termes a^n et b^n.
C'est quand meme l'oeuf avant la poule, ou la poule avant l'oeuf de passer par la somme d'une progression geometrique pour déduire la formule de l'énoncé.
Il suffit de developper le membre de droite pour arriver tout de suite sur le membre de gauche.
évidemment on te donne la réponse ... donc il suffit de développer le second membre ...
sinon (quand on va en pcsi c'est qu'on a fait une première) :::
évidemment si a ou b est nul la formule est vraie ...
on suppose alors que a n'est pas nul ... alors ::
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
gaia38 a écrit:comment vous faites pour écrire les formules comme ça?
hello
dans le forum lycée, tu as un sujet épinglé "Ecrire des belles formules mathématiques - balises TEX"
http://www.maths-forum.com/ecrire-belles-formules-mathematiques-balises-tex-70548.php
gaia38 a écrit:Punaise je comprend pas comment tu passe de la deuxième partie à la troisième (ni quoi faire après même si ça doit impliquer de transformer en une somme).
Et autre question hors sujet, comment vous faites pour écrire les formules comme ça?
j'ai appris en primaire que pour tout nombre a non nul et tout nombre b :
:zen:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
zygomatique a écrit:évidemment on te donne la réponse ... donc il suffit de développer le second membre ...
sinon (quand on va en pcsi c'est qu'on a fait une première) :::
évidemment si a ou b est nul la formule est vraie ...
on suppose alors que a n'est pas nul ... alors ::
Mais c'est quand meme relativement ridicule justement d'utiliser la somme d'une progression géométrique pour prouver ce resultat, alors que justement ce resultat c'est essentiellement la preuve de la formule donnant la somme d'une progression géométrique.
Pour calculer 1+q+q²...+q^(n-1), le plus simple c'est quand meme de multiplier par (1-q) et de voir que ca fait 1-q^n, ce qui est exactement la meme chose qu'ici.
non ce n'est pas de multiplier par 1 - q ...
si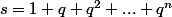 alors l'idée c'est de multiplier s par q puis la deuxième idée est de regarder pour voir et donc de le retrancher à s !!!! ... pour faire disparaître tous les termes sauf les extrêmes ...
alors l'idée c'est de multiplier s par q puis la deuxième idée est de regarder pour voir et donc de le retrancher à s !!!! ... pour faire disparaître tous les termes sauf les extrêmes ...
ensuite peut alors venir l'idée "plus complexe" de multiplier directement s par 1 - q ....
si
ensuite peut alors venir l'idée "plus complexe" de multiplier directement s par 1 - q ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
danyL a écrit:hello
dans le forum lycée, tu as un sujet épinglé "Ecrire des belles formules mathématiques - balises TEX"
http://www.maths-forum.com/ecrire-belles-formules-mathematiques-balises-tex-70548.php
merci :lol3:
EGA-SGA a écrit:Mais c'est quand meme relativement ridicule justement d'utiliser la somme d'une progression géométrique pour prouver ce resultat, alors que justement ce resultat c'est essentiellement la preuve de la formule donnant la somme d'une progression géométrique.
En fait moi sa me va très bien car on avait pas prouvé la somme avec ça, c'est pour ça que je l'avais pas vu en première cette formule.
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 90 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
