Exercice de probabilité

[kaya]

salut à tous!
j'ai du mal à achever cet exercice de probabilité:

soit la variable X à qui est associée la densité de pobabilité f(x).
où f(x)=a*e^(-a*x) si x>0 sinon f(x)=0
1-Soit Y la variable définie par
Y=[X] où [X] est la partie entière de X
a/loi de probabilit de Y
b/Calcul de Espérence math, et Variance
2-Soit Z la variable prenant la valeur de l'entier le plus proche de x
prise par X.
(même question que 1-)
3-Moindre carré (entre X et Z)

je comprend bien le problème et je peux même imaginer le genre résultat mais je n'arrive à le concrétiser comme il le faut
Si quelqu'un a une petite idée sur ce problème, ce serait sympa s'il me l'expose ici.

[Galt]

Soit k un entier. La proba que X appartienne à l'intervalle [k, k+1[ est l'intégrale de f entre ces bornes, ce qui donne , soit .
L'espérance de Y va donner la somme des , qui est classique puisqu'elle est analogue à la série de terme général avec .
Pour Z, c'est pareil sauf qu'on est dans l'intervalle ] , ] fermé ou ouvert, et que ça merde en 0.
Pour les variances c'est pareil sauf que c'est la série de terme général
Pour la somme de la série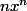 , on sait que s'écrit puis on dérive, soit , on règle les indices. On redérive pour la deuxième somme.