Exercice probabilité

[Deliantha]

Ce serait le théorème de la convergence dominée à appliquer aux espérances.

[Arkhnor]

Bonjour,

J'avoue que je ne vois pas comment appliquer le théorème de convergence dominée. Comment prouve-t-on l'hypothèse de domination ?

J'arrive à prouver que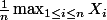 converge vers 0 en probabilité; ce qui est suffisant pour pouvoir appliquer le théorème de convergence dominée (ou de Vitali), mais je n'arrive pas à prouver l'hypothèse de domination. (ni d'uniforme intégrabilité ...)

[Deliantha]

Evoquer d'abord peut-être la loi forte des grands nombres....

[Arkhnor]

Sans avoir d'hypothèse d'indépendance ? Il y a des hypothèses quand même à la loi des grands nombres ...
Et quand bien même on ajouterait cette hypothèse d'indépendance, je ne vois pas en quoi la loi des grands nombres nous aide à prouver l'hypothèse de domination nécessaire pour appliquer le théorème de convergence dominée.

[nuage]

Voici l'énoncé;
Soit X1,X2,... des variables aléatoire négatives possédant la même distribution mais pas nécessairement indépendantes et E[X1] infini E[max i<n Xi/n]=0.

C'est faux.
Il faut supposer pour que la propriété soit vraie.
Un contre exemple sinon :
prend les valeurs avec les probas pour et

[edition] En rouge c'est une erreur grave. Mais je pense quand même que que la propriété est fausse si

[Deliantha]

La convergence de est à bâtir via avec des hypothèses tronquées sur ces V.A...On suppose la convergence presque sûre puis 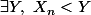et ...

[Arkhnor]

@Deliantha Les variables ne sont pas supposées être discrètes, donc ta formule pour l'espérance n'est pas applicable ici.
Il est évident que si tu rajoutes constamment des hypothèses à l'exercice, il finit par devenir trivial ...

@nuage Je pense que l'énoncé exact est "Soit X1,X2,... des variables aléatoire non négatives ..."
Je peux me tromper, mais si gérard1000 daigne repasser par ici, il pourra confirmer ou infirmer.

[Deliantha]

@Deliantha Les variables ne sont pas supposées être discrètes, donc ta formule pour l'espérance n'est pas applicable ici.
Il est évident que si tu rajoutes constamment des hypothèses à l'exercice, il finit par devenir trivial ...

Quoi qu'il en soit, des hypothèses manquent alors autant les (r)établir : la continuité ou la discrétion de la répartition ne change pas ce problème a priori si la continuité et borne de la distribution sont définies.

[Arkhnor]

Tu rajoutes des hypothèses qui rendent l'exercice totalement trivial. Ca ne présente pas grand intérêt, autant rajouter la conclusion comme hypothèse tant qu'on y est.

De plus, pourquoi sais-tu qu'il manque des hypothèses ? Car tu ne sais pas résoudre l'exercice sans celles-ci ? ...

[Deliantha]

De plus, pourquoi sais-tu qu'il manque des hypothèses ? Car tu ne sais pas résoudre l'exercice sans celles-ci ? ...

Et toi, es-tu venu à bout de cet exo jusqu'à présent ? Le comportement de pour n grand fait défaut.

[Arkhnor]

Non, je n'ai pas réussi l'exercice, mais je ne rajoute pas l'hypothèse de domination de façon ad hoc pour pouvoir appliquer le théorème de convergence dominée; et je n'en conclus pas non plus que l'énoncé est faux ...
En bref, je continue de chercher plutôt que de lancer des messages mystérieux qui n'aident personne ...

Si l'exercice est faux selon toi, pourquoi ne pas chercher un contre-exemple ?

[Deliantha]

Les interventions n'ont rien d'étrange : des données indispensables sont absentes. Quant aux contre-exemple, l'un a été fourni. Autant explorer les pistes possibles en mode arborescent où l'ironie n'aide pas.

[Arkhnor]

En quoi le contre-exemple a-t-il été fourni ? nuage a admis avoir fait une erreur dans son raisonnement ...

[Deliantha]

En quoi le contre-exemple a-t-il été fourni ? nuage a admis avoir fait une erreur dans son raisonnement ...

Il a bâti lui-même ses présupposés. Laisse en émerger d'autres en ne bloquant pas le cours des réflexions.

[Arkhnor]

Totalement délirant. Tu ne veux pas chercher de contre-exemple car tu dis qu'il y en a déjà un; on te montre qu'il n'y en a pas, et c'est moi qui bloque les réflexions.

Tu n'as toujours pas expliqué pourquoi la loi des grands nombres pourrait jouer un rôle.
Moi aussi, je peux lancer des noms de théorèmes pour faire bien si je voulais ...

Enfin, bref, inutile de polémiquer plus longtemps, et concentrons nous sur l'exercice : recherche d'un éventuel contre-exemple, hypothèses (raisonnables !) à rajouter s'il en manque, et résolution.

[Deliantha]

La loi des grands nombres permet d'avoir la moyenne empirique en estimateur convergent avec pour . En général, les valeurs des fonctions caractéristiques (impliquant les moments) des suites de v.a. sont conditionnées par les convergences (qu'elles soient spatiales, en probabilité ou lois). Ce que tu assimiles au délire s'appelle la créativité divergente fondamentale à la construction mentale. Gare à ne pas transférer en détracteur de principe ses propres carences d'idées par effet miroir sur l'interlocuteur.

[Arkhnor]

Epargne-nous tes délires ...

Que viennent faire les fonctions caractéristiques maintenant ? Et les moments ? Tu cherches à étaler ta culture ? ...

[Deliantha]

Que viennent faire les fonctions caractéristiques maintenant ? Et les moments ? Tu cherches à étaler ta culture ? ...

Un complexe en déroute ? Un rappel des notions sur les v.a. fera ainsi l'affaire pour autrui à l'abordage.

[Arkhnor]

Merci pour les rappels, j'en avais grandement besoin ... :dodo:

Peut-être que maintenant, tu voudras nous dire en quoi la loi des grands nombres, les moments et les fonctions caractéristiques sont utiles pour l'exercice ici présent.
Je n'espère absolument aucune réponse de ta part, ce n'est que la 3ème ou 4ème fois que je pose cette question ...