normalement,
Faut donc s'intéresser au calcul de la somme du second terme.
on a
Posons
On a
Il reste a calculer
Exercice probabilité Prepa ECS
32 messages
- Page 2 sur 2 - 1, 2
par fatal_error » 03 Jan 2009, 16:49
re,
 = (a+b+1)\sum p[Y=k] - \sum (a+b+1 -k) p[Y=k])
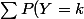normalement,=1)
Faut donc s'intéresser au calcul de la somme du second terme.
on a!}{(a+b-k-(a-1))!(a-1)!})
Posons
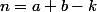
et 
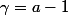
On a!}{(n-\gamma)!(\gamma)!}=\sum \frac{(n+1)!}{((n+1)-(\gamma +1))!(\gamma)!}=\sum \frac{(n+1)!(\gamma +1)}{(\gamma +1)!((n+1)-(\gamma+1))!}=\sum (\gamma +1) C_{n+1}^{\gamma+1}=\sum aC_{a+b-k+1}^{a})
Il reste a calculer
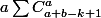
mais la comme ca j'ai pas d'idées
normalement,
Faut donc s'intéresser au calcul de la somme du second terme.
on a
Posons
On a
Il reste a calculer
la vie est une fête 
par fatal_error » 03 Jan 2009, 16:54
En étape d'aide/vérif,
sachant que=\frac{a+b+1}{a+1})
On identifie avec notre résultat :
=(a+b+1)-x)
x etant la somme qu'on essaie de calculer.
On doit trouver(a+1)-(a+b+1)}{a+1})
cad
C_{b}^{a}}{a+1})
cad on veutC_{b}^{a}}{a+1})
sachant que
On identifie avec notre résultat :
x etant la somme qu'on essaie de calculer.
On doit trouver
cad
cad on veut
la vie est une fête
par fatal_error » 03 Jan 2009, 20:29
sigma(variant de k=A à B) de A parmi k vaut A+1 parmis B+1.
La formule qui m'aura fait pousser des boutons !!!
On a donc :
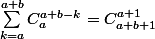
On utilise le dénominateur :
!a!b!}{(a+1)!b!(a+b)!}=\frac{a+b+1}{a+1})
è_é
La formule qui m'aura fait pousser des boutons !!!
On a donc :
On utilise le dénominateur :
è_é
la vie est une fête
par fatal_error » 03 Jan 2009, 20:42
En relisant le poste je suis tombé sur la formule
sigma(variant de k=A à B) de A parmi k vaut A+1 parmis B+1.
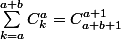
On utilise le dénominateur :
è_é
Maintenant, faut arriver a faire le changement d'indice adéquat qui relie
Si k varie de a à a+b, alors on doit avoir a+b-j+1 varie de a, a+b
donc j varie de 1 a b+1. Est-ce le cas?
sigma(variant de k=A à B) de A parmi k vaut A+1 parmis B+1.
On utilise le dénominateur :
è_é
Maintenant, faut arriver a faire le changement d'indice adéquat qui relie
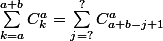
Si k varie de a à a+b, alors on doit avoir a+b-j+1 varie de a, a+b
donc j varie de 1 a b+1. Est-ce le cas?
la vie est une fête
par dark7rider » 04 Jan 2009, 16:05
En fait, je ne comprend pas bien ce que tu as fait dans ton post précédent. J'ai bien compris jusu'à "cad on veut..." mais ton post suivant, je ne comprend pas trop ce que tu fais...
par dark7rider » 04 Jan 2009, 16:17
parceque je vois comment tu obtiens a+1 parmis a+b+1 en faisant un changement d'indice, k = a+b-k+1. Mais ensiute tu divises par quelque chose et je ne comprend pas en quoi ca prouve ce qu'on cherchait
par dark7rider » 04 Jan 2009, 16:30
okkkk jai compris, tu avais oublié le a parmis a+b c'est pour ca,,, je viens de remarquer!!
par dark7rider » 04 Jan 2009, 19:41
et au fait, si ca tinteresse, j'ai trouvé un moyen facile de faire la question de E(X)
par dark7rider » 10 Jan 2009, 22:09
ba en fait, en exprmimant tout simplement lesperance, on trouve une somme de kp^k-1
sauf que c'est pas p ou je sais plus trop,ca remonte maintenant. Et ca, c'est la dérivée de p^k donc en fait ca va tout dseul
sauf que c'est pas p ou je sais plus trop,ca remonte maintenant. Et ca, c'est la dérivée de p^k donc en fait ca va tout dseul
32 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :