Exercice probabilité

[Deliantha]

J'ai répondu : apprends à lire sur nos lignes...Et pour un dialogue en chat : 3615 CODE DIX ! :ptdr:

[Arkhnor]

La loi des grands nombres permet d'avoir la moyenne empirique en estimateur convergent avec n pour E(X_n). En général, les valeurs des fonctions caractéristiques (impliquant les moments) des suites de v.a. sont conditionnées par les convergences (qu'elles soient spatiales, en probabilité ou lois).

Il est vrai que le lien avec l'exercice est clair comme de l'eau de roche ... Je l'ai déjà dit : parler des fonctions caractéristiques et des moments ici n'amène à rien, à part étaler ta culture.
Tu ne veux pas répondre, libre aux autres d'en conclure que tu ne sais pas répondre.

[Deliantha]

Il est vrai que le lien avec l'exercice est clair comme de l'eau de roche ...

En effet, libre à cha(t)cun de constater qu'on quête des noises en guêpe au lieu de s'atteler aux sens.

[fatal_error]

blr,

quelqu'un pour m'expliquer dans
[quote]Soit X1,X2,... des variables aléatoire négatives possédant la même distribution mais pas nécessairement indépendantes et E[X1] infini E[max iinfini E[max i<n Xi/n]=0 signifie?

Supposons X1=[1,2,3], X2=[2,3,1]

ce que je pige pas c'est E[max i<n Xi/n], l'espérance prend en argument une variable aléatoire.
Donc max i<n Xi/n doit être une variable aléatoire.
On peut factoriser le n:
1/n max i<n Xi
Comment choisir max i<n Xi, qu'est-ce qui me définit que X1<X2?

qqch me dit que je comprends mal l'énoncé, un éclairement?

[Arkhnor]

sont des variables aléatoires, c'est à dire des fonctions définies sur un espace probabilisé. Si est l'espace probabilisé, est une fonction de dans .

Si sont des fonctions à valeurs réelles définies sur un ensemble E, on définit leur maximum par

Cette définition vaut aussi pour les variables aléatoires, puisque ce sont des fonctions.

est donc la variable aléatoire qui à tout associe .

[Arkhnor]

Exemple : Si représente la valeur obtenue au -ème lancer d'un dé, alors représente la valeur maximale obtenue après lancers.

[fatal_error]

merci pour l'éclaircissement.
Ton deuxième example est différent, puisqu'il s'agit simplement d'un cas 1D, prendre le max sur une série de valeur.

Le cas que tu avais expliqué, est plutot 2D, pour chaque valeur w, prendre le max de Xi(w).

Il reste une dernière question...l'énoncé dit
variables aléatoire possédant la même distribution

si on considere l'espace probabilisé (W,{1, 2, 3}, P) (je suis pas à l'aise avec ça)
et qu'on prend X1:
P(X1=1)=0.5
P(X1=2)=0.25
P(X1=3)=0.25
X1 de même distribution que X2 représente donc
P(X2=1)=0.5
P(X2=2)=0.25
P(X2=3)=0.25
non?

De fait pour w dans {1,2,3}
on a max(X1,X2)=X1=X2 vu que pour w donné, X1(w)=X2(w)

[Arkhnor]

Ton deuxième example est différent, puisqu'il s'agit simplement d'un cas 1D, prendre le max sur une série de valeur.

Le cas que tu avais expliqué, est plutot 2D, pour chaque valeur w, prendre le max de Xi(w).

Absolument pas. Comme je l'ai dit, une variable aléatoire est une fonction définie sur un espace probabilisé, et la seule façon de définir le maximum d'une famille de fonctions, c'est la définition que j'ai donnée.

Evidemment, quand on dit " représente la valeur obtenu au ème lancer de dés", on masque complètement la nature mathématique de l'objet : on masque l'espace probabilisé, on masque le fait que soit une fonction.
Mais ça n'empêche pas que ces objets là existent, et que c'est à eux qu'on doit référer lorsqu'on applique des opérations mathématiques (comme la somme, la multiplication, la prise de maximum, etc) à des variables aléatoires.

Dans l'exemple que tu donnes, , et donc le max des deux est égal aussi bien à qu'à . Mais c'est un cas très exceptionnel. (on est par exemple très loin d'avoir indépendance entre les deux variables)

[Arkhnor]

Pour reprendre l'exemple de mes dés, et montrer que cet exemple est bien un exemple pour la définition du max que j'ai donné, je mets les détails, dans le cas de deux lancers indépendants de deux pièces non truquées.

Je note pile par 0, et face par 1.

On prend l'espace , muni de la tribu de l'ensemble des parties, et de la probabilité uniforme.

Tout élément de est un couple avec et appartenant à .

Alors, l'application qui à associe est une variable aléatoire qui représente le lancer d'une pièce. (on vérifie que
De même, qui à associe représente le lancer d'une autre pièce.

On a donc et

On peut vérifier que et sont indépendantes.

Si on calcule , on a : ; ; et de même .

[Doraki]

Je suppose comme Arkhnor que dans l'énoncé on suppose que les Xi sont positives.
(si elles sont négatives, alors 0 >= E(max_(i= E(X1/n) = E(X1)/n, et comme E(X1)/n tend vers 0, E(max ...) tend aussi vers 0)

Pour x dans [0;1], soit fi(x) = Sup {E(Xi*Y), où Y est une variable dans [0;1] d'espérance <= x.
Ce sup est fini car E(Xi) est finie : fi(x) <= fi(1) = E(Xi) < infini.
fi est croissante, dérivable presque partout (je crois), concave, ne dépend que de la loi de Xi, (fi' est à peu près la réciproque de la fonction de répartition de Xi)
et par le théorème de convergence dominée, sa limite en 0 vaut 0.

Pour tout n et i<=n, soit e(i,n) l'événement "X1, ..., X(i-1) < Xi et X(i+1), ..., Xn <= Xi", c'est à dire que i est l'indice du maximum de X1...Xn, et en cas d'égalités, c'est le plus petit indice.
Soit p(i,n) = P(e(i,n)) = E(1_e(i,n)).
les événements e(i,n) lorsque i parcourt {1..n} forment une partition de l'univers, donc p(1,n)+...+p(n,n) = 1, et on a
E(max(X1...Xn)) = E(X1*1_e(1,n) + ... + Xn*1_e(n,n)) <= f1(p(1,n)) + ... + fn(p(n,n)) = f1(p(1,n)) + ... + f1(p(n,n)) <= n*f1(1/n) (par concavité de f1).
Donc E(max(X1...Xn))/n <= f1(1/n), qui tend vers 0 quand n tend vers l'infini.

[Arkhnor]

correspond à l'inverse généralisé de la fonction de distribution ?

est défini sur le même espace que les ? Pas besoin d'agrandir l'espace probabilisé ?
J'essaye de voir pourquoi le sup ne dépend que de la loi. (a priori, peut dépendre de )

J'avais essayé l'approche classique de décomposer l'espace, comme on fait d'habitude pour des inégalités maximales; mais j'étais très vite resté bloqué.

Si c'est correct, c'est très élégant : pas besoin d'invoquer des théorèmes puissants, ni d'ajouter des hypothèses à l'emporte pièce.

[Doraki]

Ben toute la difficulté est cachée dans les propriétés de fi.

Je crois pas qu'il y ait besoin d'agrandir l'espace probabilisé, parceque je fais varier une variable aléatoire plutôt qu'un événement (au début je regardais seulement les Y = fonctions caractéristiques d'événements mais en fait, c'était nul et je devais faire ce genre d'artifice).

La concavité était fatigante à montrer avec des fonctions caractéristiques ; avec des variables il suffit de prendre la moyenne des n variables et ça tombe tout seul.

Le seul vrai truc dur est que f dépende seulement de la loi de X.
Pour x dans R, soit p(x) = P(X>=x).
On a donc en prenant Y = 1_{X>=x}, f(p(x)) >= E(X*1_{X>=x}).
Si Z est une autre variable différente de Y, alors Z s'écrit Y + Z1 - Z2 où Z1 = 0 lorsque X>=x et Z2 = 0 lorsque X=x}), et au passage on obtient une suite de variables Y qui montrent que la limite en 0 vaut 0.

Ensuite il peut y avoir des atomes, et ça donne des bouts de segments à rajouter dans le graphe.
Cette fois on prend des Y de la forme y*1_{X=x} + 1_{X>x} où y varie dans [0;1] et c'est le même raisonnement juste en un peu plus long.

[Arkhnor]

Si Z est une autre variable différente de Y, alors Z s'écrit Y + Z1 - Z2 où Z1 = 0 lorsque X>=x et Z2 = 0 lorsque X<x, avec E(Z1) = E(Z2) = z.

Comment montres-tu que ? Les conditions que tu donnes avant déterminent complètement et , et à partir de leurs expressions, j'arrive à .

Rien ne dit que est nul, d'autant que prend des valeurs arbitraires.

[Arkhnor]

En revanche, si on continue le raisonnement, ça nous donne , et donc on a bien .

Très bien vu !

[Doraki]

ah oui j'ai oublié de préciser qu'on regardait un Z tel que E(Z) = E(Y) (de la même taille que Y).
Si Z est plus gros, ce qu'on fait n'a plus grand chose à voir avec f(p(x))

Et puis on devrait pouvoir remplacer mon "où Y est d'espérance <= x" par un "où Y est d'espérance x" dans ma définition ça devrait rien changer (quand j'étais sur les fonctions caractéristiques j'étais pas sûr alors j'avais prévu large)

[Arkhnor]

fi est croissante, dérivable presque partout (je crois)

Si est croissante, alors elle est dérivable presque partout par le théorème de Lebesgue. En fait, de façon plus élémentaire, on peut démontrer qu'une fonction convexe est dérivable presque partout.

[Deliantha]

X est une v.a établie positive ce qui n'est pas explicite dans cet énoncé. Mais E(X) peut être infinie si X est non intégrable (en suivant une loi de Cauchy par exemple); alors les f_i n'auraient pas de cohérence.

Les propriétés de vos f_i dépendraient surtout de l'existence supposée des E(Z_i) tels que Z_i =X_i *Y

Si est croissante, alors elle est dérivable presque partout par le théorème de Lebesgue. En fait, de façon plus élémentaire, on peut démontrer qu'une fonction convexe est dérivable presque partout.

La construction choisie de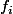 ne va -t-elle pas plutôt vers une fonction identifiée concave ?

Pour x dans [0;1], soit f_i(x) = Sup {E(Xi*Y), où Y est une variable dans [0;1] d'espérance =x).
On a donc en prenant Y = 1_{X>=x}, f(p(x)) >= E(X*1_{X>=x}).

Si désigne la fonction ou densité de répartition rien n'interdit qu'elle n'obéisse pas à la définition fournie plus haut de vos f_i, non ?

[Deliantha]

X est une v.a établie positive ce qui n'est pas explicite dans cet énoncé. Mais E(X) peut être infinie si X est non intégrable (en suivant une loi de Cauchy par exemple); alors les f_i n'auraient pas de cohérence.

Les propriétés de vos f_i dépendraient surtout de l'existence supposée des E(Z_i) tels que Z_i =X_i *Y

Si est croissante, alors elle est dérivable presque partout par le théorème de Lebesgue. En fait, de façon plus élémentaire, on peut démontrer qu'une fonction convexe est dérivable presque partout.

La construction choisie de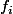 ne va -t-elle pas plutôt vers une fonction plus tôt identifiée concave ?

Pour x dans [0;1], soit f_i(x) = Sup {E(Xi*Y), où Y est une variable dans [0;1] d'espérance =x).
On a donc en prenant Y = 1_{X>=x}, f(p(x)) >= E(X*1_{X>=x}).

Si désigne la fonction ou densité de répartition rien n'interdit qu'elle n'obéisse pas à la définition fournie plus haut de vos f_i, non ? En ce cas, le contre-exemple trouvé demeure sous-jacent.

[Arkhnor]

En ce cas, le contre-exemple trouvé demeure sous-jacent.

Mais quel contre-exemple ? Personne n'a trouvé de contre-exemple. Il n'y en a pas ! Relis le message de nuage ou change de lunettes ...

X est une v.a établie positive ce qui n'est pas explicite dans cet énoncé

Si les variables sont négatives et d'espérance non égales à , l'exercice est trivial comme l'a remarqué Doraki.
Il a donc supposé, tout comme moi, que les variables sont non négatives (en bon français, on dit plutôt positives)

Mais E(X) peut être infinie si X est non intégrable

L'énoncé stipule que l'espérance des variables est finie.

La construction choisie de f_i ne va -t-elle pas plutôt vers une fonction plus tôt identifiée concave ?

Si est concave, est convexe et on applique donc le résultat que je cite à : on obtient la dérivabilité de , ce qui entraîne la dérivabilité de . Ca va, c'est suffisamment détaillé ? Ou faut-il que j'explique le passage où je multiplie par ?

Les propriétés de vos f_i dépendraient surtout de l'existence supposée des E(Z_i) tels que Z_i =X_i *Y

Pas compris.

Si f(x) = \bigsum_{i=0}^{n} f_i ? désigne la fonction ou densité de répartition rien n'interdit qu'elle n'obéisse pas à la définition fournie plus haut de vos f_i, non ?

Toujours pas compris. Quel est le problème ? On a montré que tous les sont égaux.

[Deliantha]

Mais quel contre-exemple ? Personne n'a trouvé de contre-exemple. Il n'y en a pas ! Relis le message de nuage ou change de lunettes ...

C'est à vous de mieux relire l'énoncé émis car ma vue est excellente et je ne porte pas de lunetttes.
, rien des espérances des X_i et en outre, les v.a sont ici supposées toutes négatives.
Mon contre-ex se présente pour une fonction de répartition respectant la loi de Cauchy sans .
L'attittude est un brin inacceptable vu l'agacement indu: ne te crois pas obligé de réagir sinon, hein?