Espace affine

par **RadarX** » 23 Aoû 2006, 14:36

Bonjour,

RAPPELS: A est un est esp affine attaché a un ev E (E, +) agit fidelement ettransitivement sur A.
Autrement dit on a une app AXE ---->A t. q. (M, V) ---> M+V avec
*

(ce qui exprime la transitivité)
*

(ceci exprime le fidelité de l'action.

PROBLEME: On affirme alors que qq soit

, il exite un unique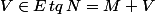

Démontrer l'unicité du V me pose un petit pb.
Et par ailleurs j'aimerais savoir comment en LaTeX on cree l'espace et le symbole mathematique "qq soit".

De rapides contrib des illustres forumistes que vous etes m'obligeraient.

par **tize** » 23 Aoû 2006, 14:42

Que veux tu dire par "l'espace" ?
pour qqsoit il y a \forall :

Pardon, pour faire un espace il y a plusieurs facon :\, ou \; ou \: ou \quad ou \qquad, il crée tous des espaces de tailles differentes ou alors \hspace{3cm} pour faire un espace de 3 cm

par **RadarX** » 23 Aoû 2006, 14:48

tize a écrit:Que veux tu dire par "l'espace" ?

Comprend pas ta question? Espace c'est espace (ensemble), c'est tout!

par **tize** » 23 Aoû 2006, 14:50

j'ai modofié mon dernier post cela repond ptet a ta question ?

par **RadarX** » 23 Aoû 2006, 14:56

tize a écrit:Que veux tu dire par "l'espace" ?
Pardon, pour faire un espace il y a plusieurs facon :\, ou \; ou \: ou \quad ou \qquad, il crée tous des espaces de tailles differentes ou alors \hspace{3cm} pour faire un espace de 3 cm

Ah oui je vois now! tu parles de la 2é partie de ma question (LATEX) je voulais dire barre d'espace: espace de separation.
Merci pour qq soit; tu peux d'ailleurs voir que j'ai corrigé mon texte.

par **tize** » 23 Aoû 2006, 14:56

Au fait, où as-tu trouvé cette definition d'espace affine ?
J'en ai une autre...

par **RadarX** » 23 Aoû 2006, 15:01

tize a écrit:Au fait, où as-tu trouvé cette definition d'espace affine ?
J'en ai une autre...

Dictionnaire de math (PUF) bOUVIER, GEORGE, LE LIONNAIS.

par **tize** » 23 Aoû 2006, 15:14

Il doit y avoir un truc du genre : si M et N appartienent à A et U est dans E,
M+U=N s'écrit aussi N-M=U. Cela permet d'avoir une application de A² dans E (M,N)->VecteurMN=N-M (je sais pas comment on fait les fleches de vecteurs).
Donc si M+U=M+V=N alors N-M=U=V ?

par **jose_latino** » 23 Aoû 2006, 15:18

Il faut utiliser les deux axiomes:

Existence: Par le prémier axiome: On a comme , il existe tel que
Unicité: Je crois que le deuxième axiome est:
Si et sont tels que alors , et on a besoin d'une asociativité:

Confirme, s'il te plaît, la définition du livre.

par **RadarX** » 23 Aoû 2006, 15:24

tize a écrit:Il doit y avoir un truc du genre : si M et N appartienent à A et U est dans E,
M+U=N s'écrit aussi N-M=U. Cela permet d'avoir une application de A² dans E (M,N)->VecteurMN=N-M (je sais pas comment on fait les fleches de vecteurs).
Donc si M+U=M+V=N alors N-M=U=V ?

A etant un esp qqcque N-M n'y a pas de sens; il n'y a pas d'operation.
On precise seulement que cet unique V tq N = M+V est noté vect(MN)

A ce propos une balise TEX pour avoir un vecteur avec la fleche sur la lettre: je prendrais bien.

par **tize** » 23 Aoû 2006, 15:29

Alors il doit y avoir associativité non ?

par **RadarX** » 23 Aoû 2006, 15:34

tize a écrit:Alors il doit y avoir associativité non ?

Ah oui, pour une action, il y a l'associativité externe toujours! M + (V+U) = (M+V) + U M A et U et V E.

Et je suis d'autant plus embeté que 'avais prouvé ce resultat il y environ 6 mois et sans pb!

par **jose_latino** » 23 Aoû 2006, 15:39

Nous pouvons montrer que les définitions du
Wikipédia
et celle que tu as donné mais en modifiant le deuxième axiome, et avec la associativité, ça veut dire:

satisfie:

Pour chaque : (Transitivité)
Si et sont tels que , alors (Fidélité)
m+(u+v)=(m+u)+v (Associativité)

sont équivalentes! :triste: mais il faut changer le deuxième axiome comme ici.

par **RadarX** » 23 Aoû 2006, 16:33

jose_latino a écrit:Nous pouvons montrer que les définitions du
Wikipédia
et celle que tu as donné mais en modifiant le deuxième axiome, et avec la associativité, ça veut dire:
satisfie:
Pour chaque : (Transitivité)
Si et sont tels que , alors (Fidélité)
m+(u+v)=(m+u)+v (Associativité)
sont équivalentes! :triste: mais il faut changer le deuxième axiome comme ici.

NON la fidelité signifie que si

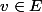
et si

,

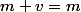
, alors

.
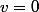
En d'autres termes, O est le seul vecteur de E qui laisse invariant tous les m de A.

par **Vedeus** » 23 Aoû 2006, 23:18

(1) Démo avec du recul sur les concepts :

Comme le groupe E est abélien et que l'action est transitive, tous
les éléments de A ont même stabilisateur F
(rappelons que de manière générale, deux éléments d'une même orbite
ont des stabilisateurs conjugués).

Par suite, les éléments de F fixent tous ceux de A, et comme l'action est fidèle,
ceci impose F={0}. On en déduit le résultat annoncé.

(2) Démo sans recul sur les concepts :

On suppose qu'il existe deux vecteurs V et V' tels que M+V=M+V'.
En posant V_1=V-V', on a donc M+V_1=M.
Mais alors, pour tout élément N de A, en choisissant un vecteur U tel que
N=M+U, on trouve que N+V_1=(M+U)+V_1=M+(U+V_1)=M+(V_1+U)
=(M+V_1)+U=M+U=N. Ceci étant valable pour tout point N, on déduit de la
fidélité de l'action que V_1 est le vecteur nul, et donc V=V'.

par **RadarX** » 27 Aoû 2006, 17:00

Vedeus a écrit:(1) Démo avec du recul sur les concepts :

Comme E est abélien et que l'action est transitive, tous les éléments de A ont même stabilisateur F.
(rappelons que de manière générale, deux éléments d'une même orbite
ont des stabilisateurs conjugués).

Par suite, les éléments de F fixent tous ceux de A, et comme l'action est fidèle, ceci impose F={0}. On en déduit le résultat annoncé.

(2) Démo sans recul sur les concepts :

On suppose qu'il existe 2 vecteurs V et V' tels que M+V=M+V'.
En posant V1=V-V', on a donc M+V1=M.
Mais alors, pour tout N A, en choisissant un vecteur U tel que
N=M+U, on trouve que N+V1=(M+U)+V_1=M+(U+V1)=M+(V1+U)
=(M+V1)+U=M+U=N. Ceci étant valable pour tout point N, on déduit de la
fidélité de l'action que V1 est le vecteur nul, et donc V=V'.

Tes demo m'ont l'air d'etre correctes Vedeus. Enfin!
Une petite prime: La 1ere demo est ELEGANTE :we:.

Par contre les sources de jose et les miennes divergent en ce qui concerne la definition de la fidelité.

MERCI.

Espace affine

Espace affine

suis embeté

Définition équivalente

Qui est en ligne