Espace affine de dimension infinie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
azf
 par azf » 28 Nov 2021, 18:53
par azf » 28 Nov 2021, 18:53
Bonjour
Est-il absurde de dire cela à propos de la combinaison affine exprimant le point P :
Soit
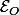
un espace affine muni d'une structure de R-espace vectoriel d'origine

de dimension infinie
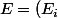_{i\in \mathbb {N}})
une famille infinie de points
affinements indépendants donc engendrant un sous-espace affine de dimension infinie
et
_{i\in \mathbb {N}})
une famille infinie de scalaires de K telle que
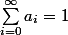
On considère un point

de
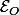
défini par la combinaison affine
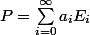
Il me semble que ce n'est pas absurde car il y a
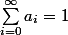
mais je me méfie
-
mathelot
 par mathelot » 28 Nov 2021, 19:13
par mathelot » 28 Nov 2021, 19:13
Bonsoir azf,
je crois me souvenir que même pour un e.v de dimension infinie,les combinaisons lineaires sont finies. Après ,si l'on veut une combinaison linéaire infinie,on a les espaces de Hilbert
-
azf
 par azf » 28 Nov 2021, 19:19
par azf » 28 Nov 2021, 19:19
Merci Mathelot
Bon bah je vais laisser ça en blanc sur mon cahier de géométrie car il faut que j'avance et je verrai ça plus tard (je refais tout en géométrie mais bon j'évite de dire des bêtises et le mieux est de laisser en blanc ce dont je ne suis pas certain)
Encore merci à toi
-
azf
 par azf » 28 Nov 2021, 19:40
par azf » 28 Nov 2021, 19:40
mathelot a écrit: Après ,si l'on veut une combinaison linéaire infinie,on a les espaces de Hilbert
Ah oui je me rends un peu compte du problème (mais juste un peu compte)
Déjà il faut que je lui donne une structure topologique pour essayer de dire des choses comme ça
ça donc ça dépasse largement le cadre de mon cahier (et mon niveau en maths)
Encore Merci Mathelot tu m'a évité d'écrire des grosses stupidités alors même que j'essaye de refaire toute ma géométrie en enlevant les bêtises que j'avais écrit
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités