Bonjour,
J'aimerais avoir un peu d'aide concernant les équations différentielles d'ordre 2 à second membre, lorsque le discriminant est négatif.
Par exemple, en voici une :
;););)+2;);)+5;)=5cos(2;));)3sin(2;)) que l'on nommera E.
Là je comprends la procédure de comment trouver une équation caractéristique, finalement on trouve comme équation caractéristique : ;)^-x * (;)1 cos(2;)) + ;)2 sin(2;))).
C'est ensuite que je ne comprends plus comment trouver le degrés de l'équation particulière, puisque le discriminant est négatif. Dans la correction que je possède, il est écrit ";) = 2 et 2;) nest pas une racine de léquation caractéristique". Mais d'où sortent ce 2 et ce 2i ?
Merci d'avance pour votre réponse.
Equa diff ordre 2 : discriminant négatif
8 messages
- Page 1 sur 1
Stéphanois57 a écrit:Bonjour,
J'aimerais avoir un peu d'aide concernant les équations différentielles d'ordre 2 à second membre, lorsque le discriminant est négatif.
Par exemple, en voici une :;);)+2;);)+5;)=5cos(2;));)3sin(2;)) que l'on nommera E.
Là je comprends la procédure de comment trouver une équation caractéristique, finalement on trouve comme équation caractéristique :^-x * (;)1 cos(2;)) +
2 sin(2;))).
C'est ensuite que je ne comprends plus comment trouver le degrés de l'équation particulière, puisque le discriminant est négatif. Dans la correction que je possède, il est écrit ";) = 2 et 2;) nest pas une racine de léquation caractéristique". Mais d'où sortent ce 2 et ce 2i ?
Merci d'avance pour votre réponse.
On cherche une base constituée de deux fonctions exponentielles, base de l'espace vectoriel
des solutions (équation sans second membre).
On pose donc
avec
On trouve comme solution
on peut combiner C-linéairement les solutions de manière que la base soit
constituées de deux fonctions réelles
et
Quand on résout
on obtient
ce qui conduit aux deux R-solutions
Je ne connais pas les notations de ton cours. Je risque une hypothèse (mais c'est à toi de relire ton cours pour vérifier !). Le 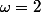 est le coefficient devant
est le coefficient devant  dans
dans ) et
et ) , et le
, et le 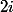 (avec
(avec 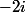 ) est le coefficient devant
) est le coefficient devant  dans l'écriture exponentielle :
dans l'écriture exponentielle : =(e^{2ix}+e^{-2ix})/2) ,
, =\ldots) .
.
Comme ni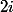 ni son conjugué
ni son conjugué 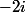 ne sont solutions de l'équation caractéristique, on cherche une solution particulière de même forme que le second membre (sans multiplication par
ne sont solutions de l'équation caractéristique, on cherche une solution particulière de même forme que le second membre (sans multiplication par  ), c.-à-d. de la forme
), c.-à-d. de la forme 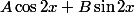 .
.
Comme ni
Bonjour à vous deux,
Tout d'abord merci beaucoup pour vos réponses rapides ! Je pense avoir compris.
Concernant l'hypothèse de Robot, il me semble qu'elle est bonne, car j'ai vérifié avec une autre équa diff, et si je prends ton raisonnement, je trouve comme à la correction. Je ne pense pas que ce soit un coup de chance si ça marche sur 2 équations différentes, donc ça doit être bon.
Encore merci, et passez un bon réveillon !
Tout d'abord merci beaucoup pour vos réponses rapides ! Je pense avoir compris.
Concernant l'hypothèse de Robot, il me semble qu'elle est bonne, car j'ai vérifié avec une autre équa diff, et si je prends ton raisonnement, je trouve comme à la correction. Je ne pense pas que ce soit un coup de chance si ça marche sur 2 équations différentes, donc ça doit être bon.
Encore merci, et passez un bon réveillon !
je ne répond pas à côté de la plaque parce que tout simplement je ne répond pas. :we:
Ce qui m'intéresse, hors résolution du problème (le problème a été tout à fait résolu),
ce sont les rapports entre les deux noyaux, l'un C-espace vectoriel et l'autre R-espace vectoriel.
de l'application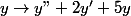
Ceci étant, j'hésitais sur la forme d'une solution particulière.
De plus, on ne lui a pas parlé de la méthode de variations des constantes
qui est un peu particulière dès que l'équation est d'ordre supérieur à 1.
Ce qui m'intéresse, hors résolution du problème (le problème a été tout à fait résolu),
ce sont les rapports entre les deux noyaux, l'un C-espace vectoriel et l'autre R-espace vectoriel.
de l'application
Ceci étant, j'hésitais sur la forme d'une solution particulière.
De plus, on ne lui a pas parlé de la méthode de variations des constantes
qui est un peu particulière dès que l'équation est d'ordre supérieur à 1.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
