Ensemble dénombrable

par **alavacommejetepousse** » 02 Déc 2009, 21:12

je n ai pas tout lu aussi

sais tu comment on montre qu une application est injective?

par **wotan2009** » 02 Déc 2009, 21:19

alavacommejetepousse a écrit:je n ai pas tout lu aussi

sais tu comment on montre qu une application est injective?

Dans le cas de mon exercice montrer que l'application est injective reviendrai à montrer qu'il y a plus d'éléments dans N que dans N². Après pour le montrer concrètement je ne sais pas trop comment m'y prendre.

par **alavacommejetepousse** » 02 Déc 2009, 21:28

non ce n est pas ça on montre que deux éléments qui ont la même image sont égaux fais le

par **Doraki** » 02 Déc 2009, 21:30

Montrer que l'application est injective, concrètement, c'est montrer qu'il n'y a pas 2 couples avec la même image :
Si on prend deux couples (x,y) et (x',y') différents (x=/=x' ou y=/=y'), alors f(x,y) est différent de f(x',y').

par **wotan2009** » 04 Déc 2009, 17:49

Doraki a écrit:Montrer que l'application est injective, concrètement, c'est montrer qu'il n'y a pas 2 couples avec la même image :
Si on prend deux couples (x,y) et (x',y') différents (x=/=x' ou y=/=y'), alors f(x,y) est différent de f(x',y').

Donc comment le montrer pour tous couple de N² ?

par **girdav** » 04 Déc 2009, 17:55

Un petit truc qui peut t'aider à mettre en forme la démonstration, même si ça a été probablement déjà dit.
Tu peut placer dans une repère quelques points de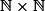

. Ensuite, en tournant la feuille d'un huitième de tour (dans le sens orienté) on voit "apparaître" une "pyramide". La donnée de

(peu importe la notation des variables) permet de savoir sur quel niveau de la pyramide on se situe, et celle de

(ou

) où se place l'image sur la ligne.

par **Ben314** » 04 Déc 2009, 18:06

Je pense que doraki voulait juste te rappeller la définition de fonction injective, je ne pense pas que ce soit une bonne voie ici vu qu'il faudra montrer que f est surjective.

La voie que je te proposait était de chercher les antécédents d'un n fixé, c'est à dire le(s) couple(s) (x,y) tels que n=x + (x + y)(x + y + 1)/2.
On va commencer par chercher s=x+y tels que n=x+s(s+1)/2.
De plus, comme on veut que y=s-x soit positif ou nul, il faut que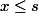

et donc que

.
Je te laisse montrer qu'il existe un UNIQUE tel s (il y a deux méthodes) puis en déduire qu'il existe un unique couple (x,y) tel que f(x,y)=n (ce qui achèvera ta démonstration).

par **wotan2009** » 04 Déc 2009, 18:12

girdav a écrit:Un petit truc qui peut t'aider à mettre en forme la démonstration, même si ça a été probablement déjà dit.
Tu peut placer dans une repère quelques points de . Ensuite, en tournant la feuille d'un huitième de tour (dans le sens orienté) on voit "apparaître" une "pyramide". La donnée de (peu importe la notation des variables) permet de savoir sur quel niveau de la pyramide on se situe, et celle de (ou ) où se place l'image sur la ligne.

Je peux dire que pour tous couples (x,y) de N² la fonction

est bijective sur l'ensemble des éléments q=x+y de N.
Est ce que ceci constitue une démonstration ?

par **wotan2009** » 04 Déc 2009, 18:30

Bon je laisse tomber cet exercice pour le moment, merci de votre aide et patience.

Ensemble dénombrable

Qui est en ligne