Ensemble dénombrable

[wotan2009]

Bonjour,
Je dois montrer que le produit cartésien de l'ensemble N avec lui même (N x N) est un ensembre dénombrable.
Pour pouvoir montrer qu'un ensemble est dénombrable il faut montrer qu'il y a une bijection entre l'ensemble donné et l'ensemble des entiers naturels N.
Il y a une indication qui dit de montrer que l'application f(x,y)= x + (x + y)(x + y + 1)/2 est bijective de NxN dans N.
Comment procéder pour montrer que pour chaque unique couple de la fonction donnée il existe un unique element dans N ?
Merci

[Doraki]

Tu veux montrer que pour tout couple (x,y) de N² il y a un unique n dans N tel que n = f(x,y) ?

Sinon, tu as regardé ce que vaut f(x,y) pour des petits entiers, par exemple pour 0 <= x,y <= 4 ?

[alavacommejetepousse]

bonjour

tu peux aussi faire un dessin pour le voir

l'application donnée permet de compter tous les couples diagonale par diagonale la première étant réduite à
(0,0) la seconde à (1,0) et (0,1) la troisième (2,0) , (1,1) , (0,2) la quatrième etc

le couple (x,y) est sur la diagonale numéro q = x+y sur laquelle il a q+1 positions

[wotan2009]

J'ai démontre donc avec 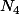et on voit bien que pour chaque couple (x,y) la fonction f(x,y) renvoie bien un unique élément de N.
f(0,0) = 0
f(0,1) = 1
f(1,0) = 2
etc... jusqu' a f(4,4). Est ce que si cela marche pour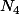 qui est une partie de N, on peut conclure que pour N cela marche aussi et que si l'ensemble 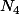x 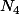dans N est dénombrable alors N x N dans N est aussi dénombrable ?

[wotan2009]

J'aurai aussi une question un peu plus générale. Par définition, un ensemble dénombrable est un ensemble dans lequel chacun des éléments de l'ensemble peut être mis en bijection avec un élément de l'ensemble N.
C'est bien les définitions mais cela ne m'aide pas vraiment à résoudre un problème concret. Quelle technique pratique permet de dénombrer un ensemble ? Comment dénombrer un ensemble concrètement ?

[Nightmare]

Salut !

Eh bien, en trouvant une bonne manière de compter ses éléments 1 par 1 ! Ici, on voit qu'il suffit de tourner un peu le plan et de compter les entiers en diagonale (c'est ce que propose la fonction).

Autre exemple pour Q : Compter des rationnels, ça revient à compter des couples d'entiers (n,m) où n est un entier relatif et m un naturel non nul (puisque tout rationnel se met bien sous la forme n/m par définition).

On a donc déjà une surjection entre ZxN* et Q. Reste à montrer que ZxN* est dénombrable.

Rien de bien difficile, compter les couples de ZxN* revient exactement à compter les entiers puisque tout entier se met sous la forme unique (penser à la décomposition en facteur premier).

[wotan2009]

Oui mais comment être sur que cette manière est la bonne manière, en particuliers avec les ensembles infinis ?

[Nightmare]

Qu'entends-tu par "bonne manière"? Si bijection il existe entre deux ensembles, elle n'est clairement pas unique donc si on arrive à compter un par un les éléments d'un ensemble, il n'y a pas qu'une façon de le faire !

[Nightmare]

Au passage, tu remarqueras que je n'ai pas vraiment mis Q et N en bijection mais seulement en injection, cela suffit bien sûr à prouver que Q est dénombrable.

[Doraki]

Par définition, un ensemble dénombrable est un ensemble dans lequel chacun des éléments de l'ensemble peut être mis en bijection avec un élément de l'ensemble N.

Les définitions, c'est bien, parceque ça permet de résoudre des problèmes concrets.

Pour être précis il faut dire qu'un ensemble dénombrable est un ensemble qui peut être mis en bijection avec N.
C'est les ensembles qui sont en bijections, pas les éléments.
dire que (2,3) est en bijection avec 17, ça veut rien dire.

Pour montrer qu'un ensemble E est dénombrable, il faut donc décrire une application de E dans N qui est bijective.
Ici, on te donne l'application de N² dans N :
Chaque élément (x,y) de N² est mis en relation avec un élément f(x,y) de N.
Il reste à montrer que f est une bijection, c'est à dire que pour tout entier n de N, il existe un unique couple (x,y) de N² tel que f(x,y) = n.

Enfin, il n'y a pas de "bonne manière" de construire des bijections entre N et un ensemble E.
Si E est dénombrable, il y a une infinité de manières de choisir une bijection entre N et E.
On se fiche pas mal de savoir précisément laquelle on prend, on veut juste savoir si il y en a ou s'il n'y en a pas.

[wotan2009]

Si je montre que pour chaque élément (x,y) de x
f(x,y) donne un unique élément, est ce que cela suffit ?

[Nightmare]

C'est qui N4 ?

[Doraki]

Ca veut dire quoi, "f(1,2) donne un unique élément" ?

[wotan2009]

= {1, 2, 3, 4}. Sinon je ne vois pas comment dire ou montrer que pour tout entier n de N il existe un unique couple (x,y) de N² tel que f(x,y) = n. Je ne vois pas comment montrer qu'il y a une bijection entre et N. Toutes les définitions que j'ai, me donne l'impression de tourner en rond.

[wotan2009]

Ca veut dire quoi, "f(1,2) donne un unique élément" ?

Qu'il n' y a qu'une seule image au couple (1,2)

[Nightmare]

Déjà, es-tu d'accord que si ce coupe existe il est unique? (ie que ton application est une injection)

[Doraki]

C'est quoi l'image du couple (1,2) ?

[wotan2009]

Déjà, es-tu d'accord que si ce coupe existe il est unique? (ie que ton application est une injection)

Oui mais si il fallait le démontrer je ne saurai pas le faire. A part en remplaçant par des valeurs concrètes.

C'est quoi l'image du couple (1,2) ?

f(1,2), un élément de N² ?

[Doraki]

f est une application de NxN dans N.
(1,2) est un élément de NxN.
f(1,2) doit être un élément de N, et je te demande quel entier c'est.

[wotan2009]

f est une application de NxN dans N.
(1,2) est un élément de NxN.
f(1,2) doit être un élément de N, et je te demande quel entier c'est.

f(1, 2) = 7