Endomorphisme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 09 Déc 2012, 14:54
par leon1789 » 09 Déc 2012, 14:54
barbu23 a écrit:Je ne sais pas. Comment le savoir ?
Peu importe, si c'est pas dit que E est de dimension 3, alors
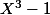
n'est pas le polynôme caractéristique, mais simplement un multiple du polynôme minimal.
Cela ne change pas ton raisonnement, mais cela évite de dire des choses fausses dans ton raisonnement.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Déc 2012, 14:58
par barbu23 » 09 Déc 2012, 14:58
leon1789 a écrit:Montre que l'un est inclus dans l'autre, et réciproquement.
 \exists a \in E $)
:
 ( a ) = x $)
Soit :
 $)
:
Il existe

tel que :
 = a + x $)
On a :
 ( x ) = ( f^2 + f + \mathrm{id}_E ) \circ ( f - \mathrm{id}_E ) ( a ) = ( f^2 + f + \mathrm{id}_E ) ( f(a) - a ) $)
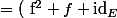 \circ f(a ) - ( f^2 + f + \mathrm{id}_E ) ( a ) $)
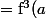 + f^2 ( a ) + f(a) - f^2 ( a ) - f(a) - a = f^3 ( a ) - a = 0 $)
Par conséquent :
 $)
.
Correct ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 09 Déc 2012, 14:59
par leon1789 » 09 Déc 2012, 14:59
oui. :zen:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Déc 2012, 15:06
par barbu23 » 09 Déc 2012, 15:06
leon1789 a écrit:oui. :zen:
Il reste à montrer que :
 \subset \mathrm{Im} ( f - \mathrm{id}_E ))
.
Soit
)
.
Alors :
 ( x ) = f^2 (x) + f(x) + x = 0)
.
Alors, comment montrer qu'il existe

tel que
 = a + x $)
? :mur: :hum:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Déc 2012, 15:18
par barbu23 » 09 Déc 2012, 15:18
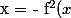 - f(x) = -f ( f(x) ) - f(x) $)
.
On pose
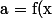 $)
.
Par conséquent :
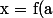 - a $)
.
Par conséquent :
 $)
.
non ?
Edit : Il y'a une erreur de signe dans le calcul. :mur:
Pouvez vous m'aider un peu sur cette question ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 09 Déc 2012, 15:24
par leon1789 » 09 Déc 2012, 15:24
pose a=-f(x) :lol3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Déc 2012, 15:26
par barbu23 » 09 Déc 2012, 15:26
ça ne marche pas même avec
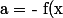 $)
. ça donne
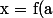 + a $)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Déc 2012, 15:28
par barbu23 » 09 Déc 2012, 15:28
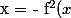 - f(x) = -f ( f(x) ) - f(x) $)
.
On pose
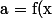 $)
.
Par conséquent :
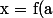 - a $)
.
Par conséquent :
 $)
.
non ?
Edit : Il y'a une erreur de signe dans le calcul. :mur:
Pouvez vous m'aider un peu sur cette question ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Déc 2012, 15:29
par barbu23 » 09 Déc 2012, 15:29
On utilise les dimensions ?

et
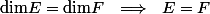
?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 09 Déc 2012, 15:29
par leon1789 » 09 Déc 2012, 15:29
Méthode 1 :
écrire une relation de Bézout entre
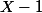
et
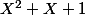
Méthode 2 :
On utilise les dimensions (comme tu as dit)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Déc 2012, 15:42
par barbu23 » 09 Déc 2012, 15:42
On essaye Bezout alors :
 \wedge ( X^2 + X + 1 ) = 1 \ \ \Longrightarrow \ \ \exists P , Q \in \mathbb{C} [X] \ : \ P(X) ( X-1 ) + Q ( X ) ( X^2 + X + 1 ) = 1 $)
 ( f - \mathrm{id} ) + Q ( f ) ( f^2 + f + \mathrm{id} ) = \mathrm{id}_E $)
 \circ ( f - \mathrm{id}_E ) ( x ) = x $)
car
 $)
, par hypothèse.
Donc,
 ( P(f) ( x ) = x $)
On pose :
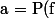 ( x ) $)
, on obtient :
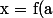 - a $)
Par conséquent
 $)
.
Correct ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 09 Déc 2012, 15:42
par leon1789 » 09 Déc 2012, 15:42
exact ! :zen:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Déc 2012, 15:43
par barbu23 » 09 Déc 2012, 15:43
leon1789 a écrit:exact ! :zen:
Merci. :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités