SEV stable par un endomorphisme nilpotent

[Aspx]

Bonjour !

Soit un -ev de dimension et un endomorphisme nilpotent d'ordre . Quels sont les SEV de stables par ?

Pour répondre à cette question je me suis d'abord mis à "réduire" .
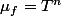
Le polynôme minimal de est manifestement et son caractéristique .

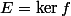
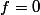
Ceci dit f ne peut être diagonalisable (seule valeur propre et on aurait alors i.e ). On ne peut donc utiliser le résultat du cours qui caractérise les SEV stables (somme directe de SEV des SEV propres)...

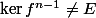
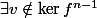
C'est pas grave... Comme on a . Ainsi de manière évidente (famille libre de cardinal ) on sait que . En particulier on a
[CENTER][/CENTER]

Voilà à peu près ce que j'ai pu en tirer, mais alors pour caractériser les SEV stables... j'ai du mal (foutue algèbre!) :briques:

Merci d'avance !

[Mohamed]

les sev stables par un endomorphime nilpotent sont ker(u^k) avec k=0..n-1...
pour l'implication indirecte c'est simple, pour l'autre implication prendre F un sev stable par u de dimension p et considérer l'endomorphisme induit, et monter que F=ker(u^p)..

[Aspx]

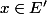
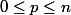
En clair il faudrait montrer que si SEV stable par de dimension , alors .

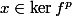
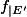
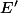
Il me semble que cela vient du fait que est la seule valeur propre de puis en écrivant un système de combinaison linéaires en prenant une base de ça pourrait être pas mal mais rien vient :hum:

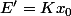
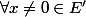
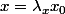
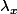
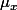
En dimension je vois bien pourquoi puisque si alors on a puis car puis en divisant par on obtient dans tous les cas (si est nul) que i.e

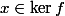
[Mohamed]

salut

soit u un endomorphisme nilpotent d'indice n
il est simple de monter que dim ker(u^k)=k , en effet on prend x tel que
u^(n-1)(x)<>0 alors on a bien vect(u^k(x),k=0..n-1) est base de E, en écrivant M la matrice de u dans cette base on voit que dim keru^k=k...

pour l'autre implication, si F est un sev de E stable par u,(dimF=p) prenons v=u/F
alors v (l'endo induit sur F) est nilpotent, soit q son indice, alors q<=p donc u^p(y)=0 pour tt y dans F, donc F est inclus dans ker(u^q) soit p<=q
On obtient alors p=q, cad F=ker(u^p).

Sauf erreur;

[Aspx]

Merci beaucoup Mohamed ! :++: