A force, j'ai peut-être une preuve qui suit plus ou moins l'ordre des questions :
On prend donc

un s.e.v. de E de dim.
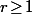
et
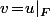
(à la source et au but).
On a
\!\subset\!F)
mais on ne peut pas avoir
\!=\!F)
vu que sinon on aurait
\!=\!F)
alors que
\!=\!\{0_E\})
.
Mais
\big)\!=\!\dim(F)\!-\!\dim\big(\ker(v)\big))
avec
\!\subset\!\ker(u))
qui est de dimension 1 donc la seule possibilité est
\!=\!\ker(u))
et
\big)\!=\!r\!-\!1)
.
Si
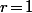
on ne fait rien de plus, et si
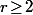
on recommence le même raisonnement : On a
\!\subset\!v(F))
mais
\!\not=\!v(F))
car sinon on aurait
\!=\!v(F)\!\not=\!\{0_E\})
. Mais
\big)\!=\!\dim(F)\!-\!\dim\big(\ker(v^2)\big))
avec
\!\subset\!\ker(u^2)\!=\!u^{-1}\big(\ker(u)\big))
qui est de dimension au plus 2 (*) donc la seule possibilité est que
\!=\!\ker(u^2))
soit de dimension exactement 2 et que
\big)\!=\!r\!-\!2)
.
etc...
(*) Dans le cas général d'une application linéaire
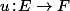
(de dim. finies), si

est un s.e.v de

alors, en considérant la restriction
\to G)
de

, on a :
\big)\!<br />=\!\dim\big(\mathrm{im}(w)\big)\!+\!\dim\big(\ker(w)\big)<br />\leq\dim(G)+\dim\big(\ker(u)\big))
